音频频谱图

背景

在本示例中，我们将逐步构建 DALI 音频处理 pipeline，包括频谱图的计算。频谱图是信号（例如音频信号）的表示，显示了频率频谱随时间的演变。

通常，频谱图是通过计算从原始信号中提取的一系列重叠窗口上的快速傅里叶变换 (FFT) 来计算的。将信号划分为固定大小的短期序列并独立地对这些序列应用 FFT 的过程称为短时傅里叶变换 (STFT)。然后，将频谱图计算为 STFT 的（通常是平方的）复数幅度。

提取原始图像的短期窗口会通过产生混叠伪影来影响计算出的频谱。这通常称为频谱泄漏。为了控制/减少频谱泄漏效应，我们在提取窗口时使用不同的窗口函数。窗口函数的一些示例包括：Hann、Hanning 等。

深入探讨我们上面提到的信号处理概念的细节超出了本示例的范围。更多信息可以在这里找到

• STFT

• 窗口函数

参考实现

为了验证 DALI 实现的正确性，我们将将其与 librosa (https://librosa.github.io/librosa/) 进行比较。

import librosa as librosa
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline
import librosa.display
import os

DALI_EXTRA_PATH 环境变量应指向 DALI extra repository 中的数据下载位置。请确保检出正确的发布标签。

Librosa 提供了一个 API 来计算 STFT，生成复数输出（即复数）。然后，通过以下方式从复数 STFT 计算功率谱就变得很简单。

test_data_root = os.environ["DALI_EXTRA_PATH"]
sample_data = os.path.join(
    test_data_root, "db", "audio", "wav", "237-134500-0000.wav"
)

# Size of the FFT, which will also be used as the window length
n_fft = 2048

# Step or stride between windows. If the step is smaller than the window length,
# the windows will overlap
hop_length = 512

# Load sample audio file
y, sr = librosa.load(sample_data)

# Calculate the spectrogram as the square of the complex magnitude of the STFT
spectrogram_librosa = (
    np.abs(
        librosa.stft(
            y,
            n_fft=n_fft,
            hop_length=hop_length,
            win_length=n_fft,
            window="hann",
            pad_mode="reflect",
        )
    )
    ** 2
)

我们现在可以通过将幅度转换为分贝来将频谱图输出转换为对数刻度。在这样做时，我们还将对频谱图进行归一化，使其最大值表示 0 dB 点。

spectrogram_librosa_db = librosa.power_to_db(spectrogram_librosa, ref=np.max)

最后一步是显示频谱图

def show_spectrogram(spec, title, sr, hop_length, y_axis="log", x_axis="time"):
    librosa.display.specshow(
        spec, sr=sr, y_axis=y_axis, x_axis=x_axis, hop_length=hop_length
    )
    plt.title(title)
    plt.colorbar(format="%+2.0f dB")
    plt.tight_layout()
    plt.show()


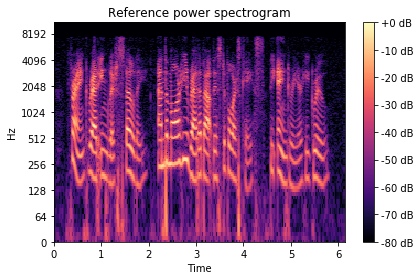
show_spectrogram(
    spectrogram_librosa_db, "Reference power spectrogram", sr, hop_length
)

使用 DALI 计算频谱图

为了演示 DALI 的 spectrogram 算子，我们将定义一个 DALI pipeline，其输入将借助 external_source 算子从外部提供。出于演示目的，我们可以在每次迭代中仅馈送相同的输入，因为我们将仅计算一个频谱图。

from nvidia.dali import pipeline_def
import nvidia.dali.fn as fn
import nvidia.dali.types as types
import nvidia.dali as dali

audio_data = np.array(y, dtype=np.float32)


@pipeline_def
def spectrogram_pipe(nfft, window_length, window_step, device="cpu"):
    audio = types.Constant(device=device, value=audio_data)
    spectrogram = fn.spectrogram(
        audio,
        device=device,
        nfft=nfft,
        window_length=window_length,
        window_step=window_step,
    )
    return spectrogram

定义了 pipeline 后，我们现在只需构建并运行它

pipe = spectrogram_pipe(
    device="gpu",
    batch_size=1,
    num_threads=3,
    device_id=0,
    nfft=n_fft,
    window_length=n_fft,
    window_step=hop_length,
)
pipe.build()
outputs = pipe.run()
spectrogram_dali = outputs[0][0].as_cpu()

并像使用参考实现一样显示它

spectrogram_dali_db = librosa.power_to_db(spectrogram_dali, ref=np.max)
show_spectrogram(spectrogram_dali_db, "DALI power spectrogram", sr, hop_length)

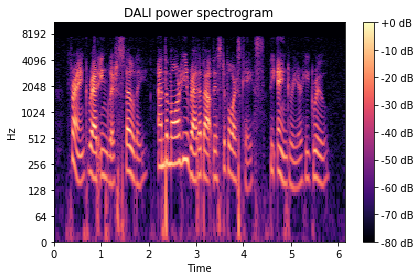
作为最后的健全性检查，我们可以验证参考实现和 DALI 的数值差异是否微不足道

print(
    "Average error: {0:.5f} dB".format(
        np.mean(np.abs(spectrogram_dali_db - spectrogram_librosa_db))
    )
)
assert np.allclose(spectrogram_dali_db, spectrogram_librosa_db, atol=2)

Average error: 0.00491 dB

Mel 频谱图

梅尔刻度是对基于音高感知的频率刻度的非线性变换。计算梅尔刻度是为了使梅尔刻度中相隔 delta 的两对频率被人类感知为等距的。更多信息可以在这里找到：https://en.wikipedia.org/wiki/Mel_scale。

在涉及语音和音频的机器学习应用中，我们通常希望以梅尔刻度域表示功率谱图。我们通过应用一组重叠的三角形滤波器来做到这一点，这些滤波器计算每个频带中频谱的能量。

通常，我们希望以分贝表示梅尔频谱图。我们可以通过使用以下 DALI pipeline 来计算以分贝表示的梅尔频谱图。

@pipeline_def
def mel_spectrogram_pipe(nfft, window_length, window_step, device="cpu"):
    audio = types.Constant(device=device, value=audio_data)
    spectrogram = fn.spectrogram(
        audio,
        device=device,
        nfft=nfft,
        window_length=window_length,
        window_step=window_step,
    )
    mel_spectrogram = fn.mel_filter_bank(
        spectrogram, sample_rate=sr, nfilter=128, freq_high=8000.0
    )
    mel_spectrogram_dB = fn.to_decibels(
        mel_spectrogram, multiplier=10.0, cutoff_db=-80
    )
    return mel_spectrogram_dB

pipe = mel_spectrogram_pipe(
    device="gpu",
    batch_size=1,
    num_threads=3,
    device_id=0,
    nfft=n_fft,
    window_length=n_fft,
    window_step=hop_length,
)
pipe.build()
outputs = pipe.run()
mel_spectrogram_dali_db = np.array(outputs[0][0].as_cpu())

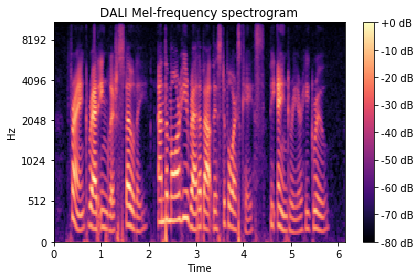
我们现在可以验证它是否产生与 Librosa 相同的结果

show_spectrogram(
    mel_spectrogram_dali_db,
    "DALI Mel-frequency spectrogram",
    sr,
    hop_length,
    y_axis="mel",
)

mel_spectrogram_librosa = librosa.feature.melspectrogram(
    y=y, sr=sr, n_mels=128, fmax=8000, pad_mode="reflect"
)
mel_spectrogram_librosa_db = librosa.power_to_db(
    mel_spectrogram_librosa, ref=np.max
)
assert np.allclose(mel_spectrogram_dali_db, mel_spectrogram_librosa_db, atol=1)

梅尔频率倒谱系数 (MFCCs)

MFCC 是梅尔频率频谱图的另一种表示形式，通常用于音频应用。MFCC 是通过对梅尔频率频谱图应用离散余弦变换 (DCT) 来计算的。

DALI 的 DCT 实现使用 https://en.wikipedia.org/wiki/Discrete_cosine_transform 中描述的公式

除了 DCT 之外，还可以应用倒谱滤波器（也称为提升）来强调更高阶的系数。

提升后的倒谱系数根据以下公式计算

\[\widehat{\text{MFCC}_i} = w_{i} \cdot \text{MFCC}_{i}\]

其中

\[w_i = 1 + \frac{L}{2}\sin\Big(\frac{\pi i}{L}\Big)\]

其中 \(L\) 是提升系数。

有关 MFCC 的更多信息可以在这里找到：https://en.wikipedia.org/wiki/Mel-frequency_cepstrum。

我们可以使用 DALI 的 MFCC 算子将梅尔频谱图转换为一组 MFCC

@pipeline_def
def mel_spectrogram_pipe(
    nfft,
    window_length,
    window_step,
    dct_type,
    n_mfcc,
    normalize,
    lifter,
    device="cpu",
):
    audio = types.Constant(device=device, value=audio_data)
    spectrogram = fn.spectrogram(
        audio,
        device=device,
        nfft=nfft,
        window_length=window_length,
        window_step=window_step,
    )
    mel_spectrogram = fn.mel_filter_bank(
        spectrogram, sample_rate=sr, nfilter=128, freq_high=8000.0
    )
    mel_spectrogram_dB = fn.to_decibels(
        mel_spectrogram, multiplier=10.0, cutoff_db=-80
    )
    mfccs = fn.mfcc(
        mel_spectrogram_dB,
        axis=0,
        dct_type=dct_type,
        n_mfcc=n_mfcc,
        normalize=normalize,
        lifter=lifter,
    )
    return mfccs

现在让我们运行 pipeline 并像之前一样显示输出

pipe = mel_spectrogram_pipe(
    device="gpu",
    batch_size=1,
    num_threads=3,
    device_id=0,
    nfft=n_fft,
    window_length=n_fft,
    window_step=hop_length,
    dct_type=2,
    n_mfcc=40,
    normalize=True,
    lifter=0,
)
pipe.build()
outputs = pipe.run()
mfccs_dali = np.array(outputs[0][0].as_cpu())

plt.figure(figsize=(10, 4))
librosa.display.specshow(mfccs_dali, x_axis="time")
plt.colorbar()
plt.title("MFCC (DALI)")
plt.tight_layout()
plt.show()

作为最后一步，让我们验证此实现是否产生与 Librosa 相同的结果。请注意，我们正在比较正交归一化的 MFCC，因为 Librosa 的 DCT 实现使用不同的公式，当我们将其与维基百科的公式进行比较时，会导致输出按 2 倍的因子缩放。

mfccs_librosa = librosa.feature.mfcc(
    S=mel_spectrogram_librosa_db, dct_type=2, n_mfcc=40, norm="ortho", lifter=0
)
assert np.allclose(mfccs_librosa, mfccs_dali, atol=1)