概述

量子计算简介

量子比特

传统（“经典”）计算机中的位可以是 0 或 1。另一方面，量子比特（“量子位”）可以表示为两种状态的线性叠加。使用狄拉克符号，这可以描述如下

\[\ket{\psi} = \alpha \ket{0} + \beta \ket{1},\]

其中 \(\ket{0}, \ket{1}\) 是正交基态，满足

\[\braket{0|0} = 1, \braket{1|1} = 1, \braket{0|1} = 0, \braket{1|0} = 0,\]

且 \(\alpha, \beta\) 是复数概率幅度，满足 \({\left| \alpha \right|}^2 + {\left| \beta \right|}^2 = 1\)。

注意

狄拉克符号，或称 bra-ket 符号，使用以下规则定义向量及其内积

  • \(\bra{\psi} = \ket{\psi}^{\dagger}\) .

  • \(\braket{\psi|\phi} \equiv (\psi, \phi) = \int\psi^* (s) \phi (s) \ ds\).

多量子比特

考虑一个由两个量子比特组成的系统

\[\begin{split}\ket{\psi_0} &= \alpha_0 \ket{0} + \beta_0 \ket{1}, \\ \ket{\psi_1} &= \alpha_1 \ket{0} + \beta_1 \ket{1}.\end{split}\]

这种两个非纠缠量子比特的量子态可以用单个量子态的张量积来描述：\(\ket{\psi_1 \psi_0} \equiv \ket{\psi_1} \otimes \ket{\psi_0}\)。

注意

克罗内克积用 \(\otimes\) 表示。使用 \(m \times n\) 矩阵 \(A = ( a_{ij} )\) 和 \(p \times q\) 矩阵 \(B = ( b_{kl} )\)，其运算由以下表达式定义

\[\begin{split}A \otimes B = \left[\begin{array}{ccc} a_{11}B & \cdots & a_{1n}B \\ \vdots & \ddots & \vdots \\ a_{m1}B & \cdots & a_{mn}B \end{array} \right].\end{split}\]

但通常，描述两个量子比特的量子态需要 4 个复数幅度

\[\ket{\psi_1 \psi_0} = \alpha_{00} \ket{00} + \alpha_{01} \ket{01} + \alpha_{10} \ket{10} + \alpha_{11} \ket{11},\]

当两个量子比特纠缠时，量子态不能写成乘积态。直接推广到 \(N\) 个量子比特得到以下表达式

\[\ket{\psi} = \sum_{p=0}^{N-1} \sum_{i_{p} \in \{0, 1\}} \alpha_{i_{N-1}i_{N-2}\cdots i_{k}\cdots i_{0}} \ket{i_{N-1}i_{N-2}\cdots i_{k}\cdots i_{0}},\]

其中 \(\alpha_{i_{N-1}i_{N-2}\cdots i_{k}\cdots i_{0}}\) 称为状态向量元素，其下标以二进制形式编码状态向量的索引。通常，需要 \(2^N\) 个概率幅度来表示 \(N\) 量子比特的量子态。

量子门

为了改变量子态，可以将各种量子门应用于组成量子比特中的一个（或多个）。考虑将 Hadamard 门 \(H = \frac{1}{\sqrt{2}}\left( \ket{0}\bra{0} + \ket{0}\bra{1} + \ket{1}\bra{0} - \ket{1}\bra{1} \right)\) 应用于状态 \(\ket{\psi} = \ket{0}\) 中的量子比特。通过此门应用，状态更改如下

\[\begin{split}\ket{\psi'} &= H\ket{\psi} \\ &= \dfrac{1}{\sqrt{2}}\left( \ket{0}\bra{0} + \ket{0}\bra{1} + \ket{1}\bra{0} - \ket{1}\bra{1} \right) \ket{0} \\ &= \dfrac{1}{\sqrt{2}}\left( \ket{0} + \ket{1} \right).\end{split}\]

每个量子门都有唯一的酉矩阵表示。在上面的示例中，运算可以写成以下表达式

\[\begin{split}H\ket{\psi} = \dfrac{1}{\sqrt{2}} \left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right] \left[\begin{array}{c} 1 \\ 0 \end{array} \right] = \dfrac{1}{\sqrt{2}} \left[\begin{array}{c} 1 \\ 1 \end{array} \right],\end{split}\]

基态 \(\ket{0}, \ket{1}\) 分别定义为两个正交向量 \(\left[1, 0\right]^{T}, \left[0, 1\right]^{T}\)。

对于多量子比特系统，应用所有相应量子比特的矩阵-向量乘法。当我们在 \(N\) 量子比特系统中应用以第 \(k\) 个量子比特为目标的 Hadamard 门时，我们得到以下结果

\[\begin{split}\left[\begin{array}{c} \alpha'_{i_{N-1}i_{N-2}\cdots 0_{k}\cdots i_{0}} \\ \alpha'_{i_{N-1}i_{N-2}\cdots 1_{k}\cdots i_{0}} \end{array} \right] = \dfrac{1}{\sqrt{2}} \left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right] \left[\begin{array}{c} \alpha_{i_{N-1}i_{N-2}\cdots 0_{k}\cdots i_{0}} \\ \alpha_{i_{N-1}i_{N-2}\cdots 1_{k}\cdots i_{0}} \end{array} \right] \text{ for } i_p \in \{0, 1\} \text{ s.t. } \ 0 \leq p \leq N-1, p \neq k.\end{split}\]

测量

当我们测量量子态时，量子态会发生变化，这称为波函数坍缩。首先，我们将考虑单量子比特的情况，然后考虑多量子比特。

  • 单量子比特

    让我们考虑单量子比特波函数 \(\ket{\psi} = \alpha \ket{0} + \beta \ket{1}\)。当我们以 Pauli-Z（计算）基测量此量子比特时，会观察到 \(\ket{0}\) 或 \(\ket{1}\)。我们观察到每种状态的概率分别由 \({\text{Pr}\left( \ket{0} \right) = \left| \alpha \right|}^2\) 和 \(\text{Pr}\left( \ket{1} \right) = {\left| \beta \right|}^2\) 给出

    • 如果观察到 \(\ket{0}\)，则幅度变为 \(\alpha = 1, \beta = 0\)，我们在测量后获得 \(\ket{\psi} = \ket{0}\)。

    • 如果观察到 \(\ket{1}\)，则幅度变为 \(\alpha = 0, \beta = 1\)，我们在测量后获得 \(\ket{\psi} = \ket{1}\)。

  • 多量子比特

    假设我们测量 \(N\) 量子比特系统 \(\ket{\psi_{N-1}\psi_{N-2}\cdots\psi_{k}\cdots\psi_{0}}\) 的第 \(k\) 个量子比特。观察每种状态的概率由概率幅度的总和定义

    • \(\ket{0}_k\) 以概率 \(\text{Pr}\left( \ket{0}_k \right) \equiv \sum_{p=0, p\neq k}^{N-1} \sum_{i_{p} \in \{0, 1\}} \left| \alpha_{i_{N-1}i_{N-2} \cdots 0_{k} \cdots i_{0}}\right|^2\) 被观察到，并且

    • \(\ket{1}_k\) 以概率 \(\text{Pr}\left( \ket{1}_k \right) \equiv \sum_{p=0, p\neq k}^{N-1} \sum_{i_{p} \in \{0, 1\}} \left| \alpha_{i_{N-1}i_{N-2} \cdots 1_{k} \cdots i_{0}}\right|^2\) 被观察到，并且

    未观察到的状态的幅度归零，而观察到的状态的幅度被归一化，使其总和等于 1；也就是说，对于 \(i_p \in \{0, 1\} \ s.t. \ 0 \leq p \leq N-1, p \neq k\)，如果观察到 \(\ket{0}_k\)，我们有以下

    \[\alpha'_{i_{N-1}i_{N-2}\cdots 0_{k}\cdots i_{0}} = \dfrac{ \alpha_{i_{N-1}i_{N-2}\cdots 0_{k}\cdots i_{0}} } { \sqrt{\text{Pr}\left( \ket{0}_k \right)}}, \quad \alpha_{i_{N-1}i_{N-2}\cdots 1_{k}\cdots i_{0}} = 0.\]

    类似地，如果观察到 \(\ket{1}_k\)，我们有以下

    \[\alpha_{i_{N-1}i_{N-2}\cdots 0_{k}\cdots i_{0}} = 0, \quad \alpha'_{i_{N-1}i_{N-2}\cdots 1_{k}\cdots i_{0}} = \dfrac{ \alpha_{i_{N-1}i_{N-2}\cdots 1_{k}\cdots i_{0}} } { \sqrt{\text{Pr}\left( \ket{1}_k \right)}}.\]

总而言之，测量量子态会导致量子相干性的丧失并使量子叠加坍缩。

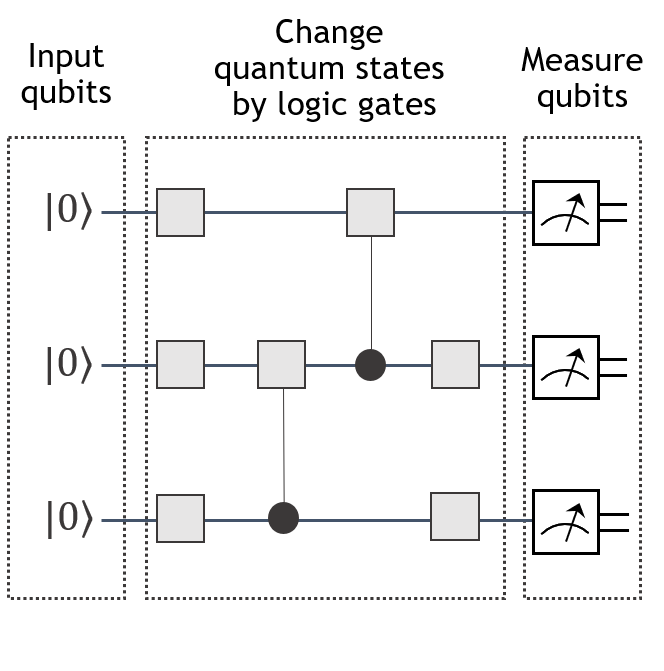
量子线路

量子计算的工作流程可以描述为量子线路。每根导线对应一个量子比特，门以从左到右的方式应用。一些门具有由黑色圆圈表示的控制位。只有当所有控制位的值与用户定义的那些值匹配时，才应用带有控制位的门。测量由程式化的指针刻度盘表示，将量子比特（单根导线）变成经典比特（双根导线）。请参见下图的代表性图示。

_images/circuit.png

量子线路模拟

在经典计算机上数值模拟量子计算的任务称为量子线路模拟。

直接的量子线路模拟可以看作是一个简单的矩阵-向量乘法。取量子线路中门序列对应的酉矩阵，并将其与表示输入状态（通常为零初始化）的列向量相乘，输出状态由结果列向量给出。cuQuantum SDK 中的 cuStateVec 库旨在为这种基于状态向量的模拟提供高性能解决方案。

然而，这种朴素的方法受到极大限制，因为问题规模随着量子比特数量呈指数级增长。此外，它没有利用任何并行性，如果只需要部分信息（例如，我们只需要期望值），则也不理想。

为了进一步超越经典计算机上可模拟的最大量子比特数（大约 50 个），我们需要探索状态向量的数据稀疏性本质。基本思想是，虽然状态向量的希尔伯特空间呈指数级增长，但并非空间的所有角落都同等重要。遵循这条路线，物理学家和数学家意识到张量网络是一种可行的策略，可以从原本无法完全描述的空间中压缩和提取相关信息。

具体来说，N 个量子比特的量子态可以被认为是 N 阶张量，它可以分解为完全收缩的低秩张量，有可能将问题的复杂度从量子比特数 N 的指数级变为多项式级。然后，主要的挑战转变为有效地计算张量收缩。cuQuantum SDK 中的 cuTensorNet 库旨在为张量网络计算提供高性能解决方案。

参考文献

NVIDIA 技术博客为进一步了解 cuQuantum SDK 提供了良好的起点

引用 cuQuantum

    1. Bayraktar 等人，“cuQuantum SDK: A High-Performance Library for Accelerating Quantum Science,” 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 2023, pp. 1050-1061, doi: 10.1109/QCE57702.2023.00119.