概述

本节介绍 cuTensorNet 库的基本工作原理。有关量子线路的通用介绍，请参阅 量子计算导论。

张量网络导论

张量网络出现在许多数学和科学领域，从量子线路模拟、量子多体物理和量子化学，到机器学习和概率论。随着网络规模呈指数级增长，越来越需要一个高性能库，它可以极大地促进跨多个领域的张量网络算法的高效并行实现，而 cuTensorNet 旨在为此服务。

张量和张量网络

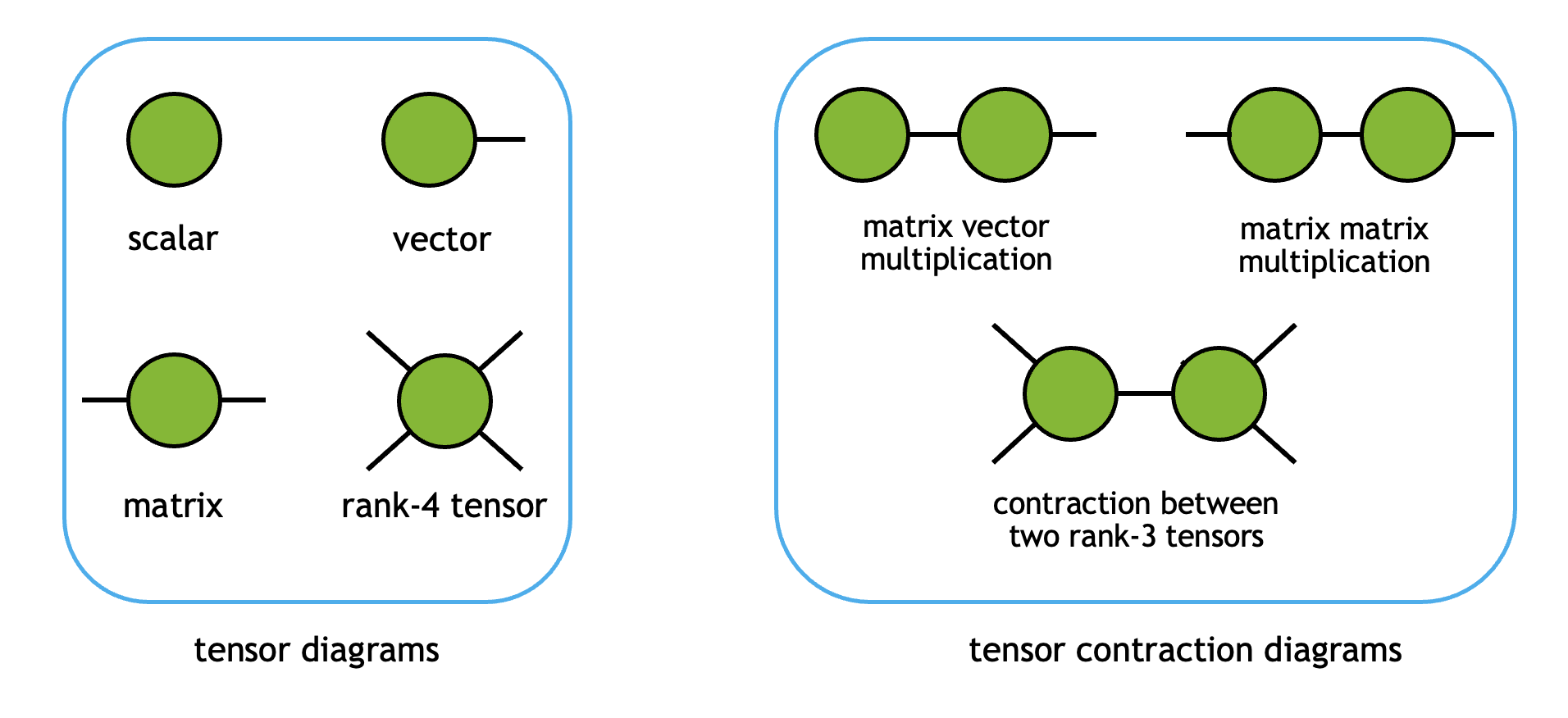
张量是将标量 (0D)、向量 (1D) 和矩阵 (2D) 推广到任意维数的概念。在 cuTensorNet 库中，我们遵循 cuTENSOR 的命名约定

  • 秩（或阶）为 \(N\) 的张量有 \(N\) 个模式

  • 每个张量模式都有一个维度（模式的大小），并且可以被分配一个标签（索引）作为张量网络的一部分

  • 每个张量模式都有一个步长，反映了沿该模式的两个逻辑上连续的元素之间在物理内存中的距离，单位为元素

例如，一个 \(3 \times 4\) 矩阵 \(M\) 有两个模式（即，它是一个秩为 2 的张量），维度分别为 3 和 4。在 C（行优先）内存布局中，它的步长为 (4, 1)。我们可以分配两个模式标签 \(i\) 和 \(j\) 来将其表示为 \(M_{ij}\)。

注意

对于 NumPy/CuPy 用户，秩/阶转换为数组属性 .ndim，维度序列转换为 .shape，步长序列的含义与 .strides 相同，但单位不同（NumPy/CuPy 使用字节而不是计数）。

当两个或多个张量被收缩以形成另一个张量时，它们共享的模式标签会被求和。从图示上看，张量及其收缩可以可视化如下

../_images/TN_diagrams.png

这里，每个顶点代表一个张量对象，每条边代表一个张量模式（标签）。当一个模式标签被收缩时，张量通过相应的边连接。

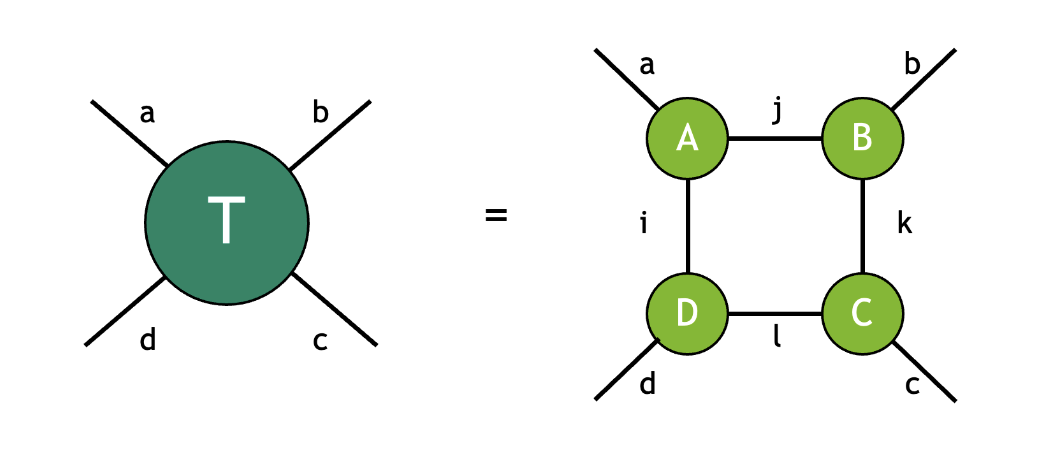
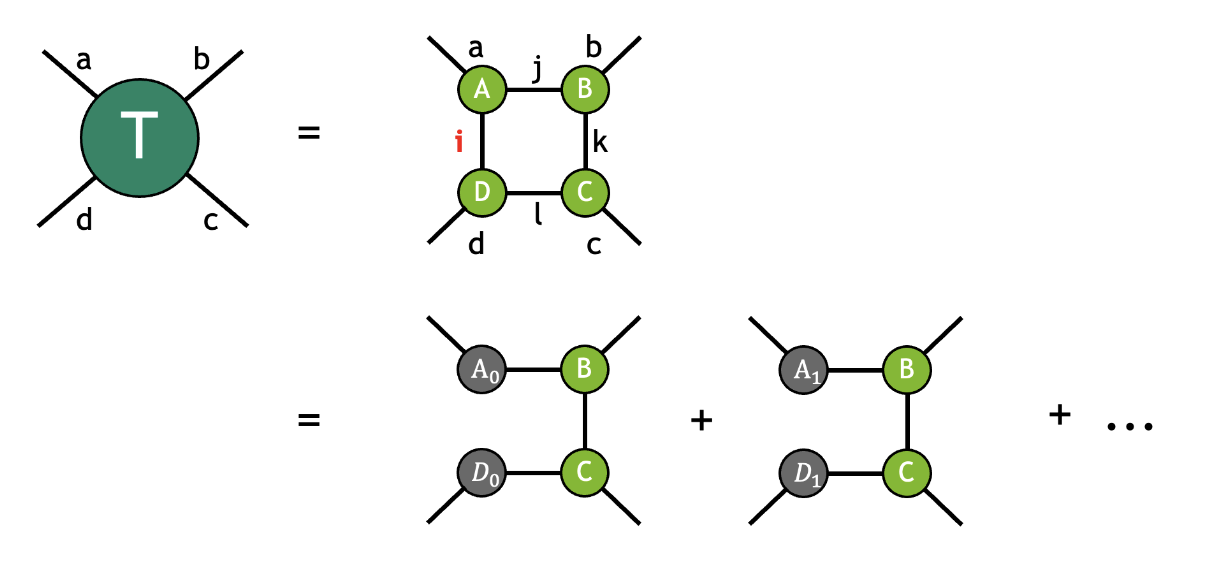
张量网络是收缩在一起以形成输出张量的张量集合。组成张量之间的收缩完全决定了网络拓扑。例如，下面的张量 \(T\) 是通过收缩张量 \(A\)、\(B\)、\(C\) 和 \(D\) 得到的

\[T_{abcd} = A_{aij} B_{bjk} C_{klc} D_{lid},\]

其中，具有相同标签的模式按照 爱因斯坦求和约定 隐式求和。在本例中，模式标签 \(i\) 连接张量 \(D\) 和 \(A\)，模式标签 \(j\) 连接张量 \(A\) 和 \(B\)，模式标签 \(k\) 连接张量 \(B\) 和 \(C\)，模式标签 \(l\) 连接张量 \(C\) 和 \(D\)。带有标签 \(a\)、\(b\)、\(c\) 和 \(d\) 的四个未收缩模式指的是自由模式（有时也称为外部模式），表明结果张量 \(T\) 的秩为 4。按照上面的图示约定，这种收缩可以可视化如下

../_images/T_ABCD.png

正如我们从图中看到的那样，这种收缩具有正方形拓扑，其中每个张量都连接到其相邻张量。

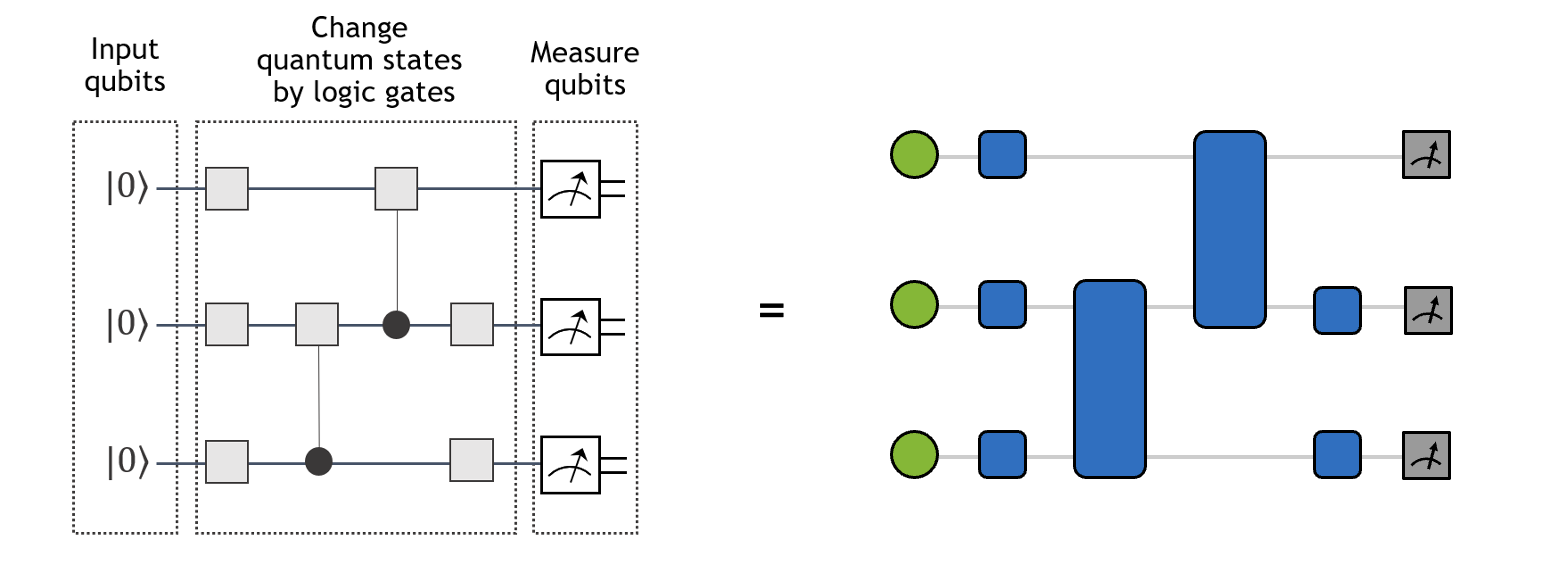
类似地，量子线路可以被视为一种张量网络。如下图所示，单量子比特门和双量子比特门分别转换为秩为 2 和秩为 4 的张量。同时，初始单量子比特状态 \(|0\rangle\) 和单量子比特测量操作可以被视为大小为 2 的向量（投影算符）。右侧张量网络的收缩产生了左侧量子线路对于特定基态（例如：\(|010\rangle\)）的波函数幅度。

../_images/QC_TN.png

张量网络的描述

给定张量网络收缩的完整描述需要两个信息：张量操作数和张量网络的拓扑结构（张量连接超图）。cuTensorNet 库中的张量网络由 cutensornetNetworkDescriptor_t 描述符表示，该描述符有效地编码了网络的拓扑图和数据类型。准确地说，此描述符指定了输入张量的数量 numInputs 以及数组 numModesIn 中每个张量的模式数量，以及指针数组 modesIn、extentsIn 和 stridesIn 中每个张量的模式、模式维度和步长。张量网络描述符还接受与每个输入张量对应的限定符数组 (qualifiersIn)，其中每个输入张量可以标记为 Conjugate（默认非 Conjugate）、Constant（默认非 Constant）和/或 requires Gradient（默认为 false）。当输入张量被标记为 Conjugate 时，其数据将在张量收缩时进行复共轭。当输入张量被标记为 Constant 时，即其数据在后续张量网络收缩中不会更改，cuTensorNet 将调用缓存机制（使用提供 CACHE 工作区内存）来加速后续张量网络收缩的计算。请参阅 中间张量的重用。当输入张量被标记为 requires Gradient 时，其对应的梯度张量将在反向传播调用时计算。同样，张量网络描述符也保存有关输出张量的类似信息（例如，numModesOut、modesOut、extentsOut、stridesOut）。请注意，每个张量网络只有一个输出张量。

所有这些网络元数据都可能驻留在主机上，因为张量网络的构建仅需要其拓扑结构和数据访问模式；在创建张量网络描述符的步骤中，我们不需要知道输入张量的实际内容。

在内部，cuTensorNet 利用 cuTENSOR 创建张量对象并执行成对张量收缩。cuTensorNet 的 API 设计使得用户可以专注于创建张量网络描述，而无需管理此类“低级”细节。张量网络收缩可以用不同的精度计算，精度由 cutensornetComputeType_t 常量给出的数据类型指定。

一旦创建了有效的张量网络，就可以

  1. 找到成本最优的张量网络收缩路径，可能带有切片和其他约束（目前，成本函数可以是总 Flop 计数或估计的求解时间）

  2. 访问有关张量网络收缩路径的信息

  3. 获取容纳中间张量所需的工作区大小

  4. 根据上面收集的信息创建张量网络收缩计划

  5. 自动调优收缩计划以优化张量网络收缩的运行时间

  6. 执行实际的张量网络收缩以生成输出张量，可以串行或并行执行

用户有责任管理工作区（来自步骤 3）以及输入/输出张量（对于步骤 5）的设备内存。有关 cuTensorNet API，请参阅 API 参考（工作区管理 API 部分）。或者，用户可以向库提供流排序内存池以方便工作区内存分配，有关详细信息，请参阅 内存管理 API。

高级张量网络规范和处理

为了简化量子科学和其他领域中遇到的张量网络的规范和处理，cuTensorNet 提供了一组高级 API 函数，供用户逐步构建给定的张量网络状态，并随后计算其属性

  • cutensornetCreateState() 用于在由其所有组成向量空间的维度指定的某个直积张量空间中创建初始（真空）张量网络状态，例如 qudit 空间，或更常见的量子比特空间（对于量子比特，所有向量空间维度都等于 2）。

  • cutensornetStateApplyTensorOperator() (cutensornetStateApplyTensor() 已弃用) 用于描述张量算符（例如，量子门）在张量网络态上的作用，以便逐步构建感兴趣的张量网络（例如，给定的量子电路），该张量网络定义了最终的张量网络态（定义的直积张量空间中的张量）。

  • 一旦构建了感兴趣的张量网络态（例如，量子电路的输出态），就可以计算其属性

    • cutensornetCreateAccessor() 指定了需要计算的张量网络态切片，以便在不生成完整状态张量的情况下检查张量网络态的幅度。

    • cutensornetCreateExpectation() 指定了给定张量网络算符在给定张量网络态上的期望值。目前，支持的张量网络算符包括那些定义为作用于张量网络态模式的不相交子集的张量乘积之和的算符。 特别是，Jordan-Wigner 变换产生此类算符的子类。 有关更多信息，请参阅 cutensornetNetworkOperator_t。

    • cutensornetCreateMarginal() 指定了要为给定张量网络态计算的边缘分布张量。 在物理学文献中，边缘分布张量被称为约化密度矩阵 (RDM)。 它是通过在指定的张量模式上，对定义的张量网络态与其共轭态（来自对偶直积张量空间）的直积进行迹运算而获得的张量。

    • cutensornetCreateSampler() 创建一个张量网络态采样器，可以对指定（全部或子集）张量模式上的张量网络态进行采样。 当对所有张量状态模式进行采样时，张量网络态定义了相应直积张量空间中的概率分布。 也就是说，每个张量元素的平方绝对值定义了其在采样过程中作为样本出现的概率。 在量子电路模拟中，这将意味着根据概率从量子电路的最终状态生成输出样本。 对不完整的张量网络态模式集进行采样将指代对相应的边缘概率分布进行采样。

近似张量网络算法

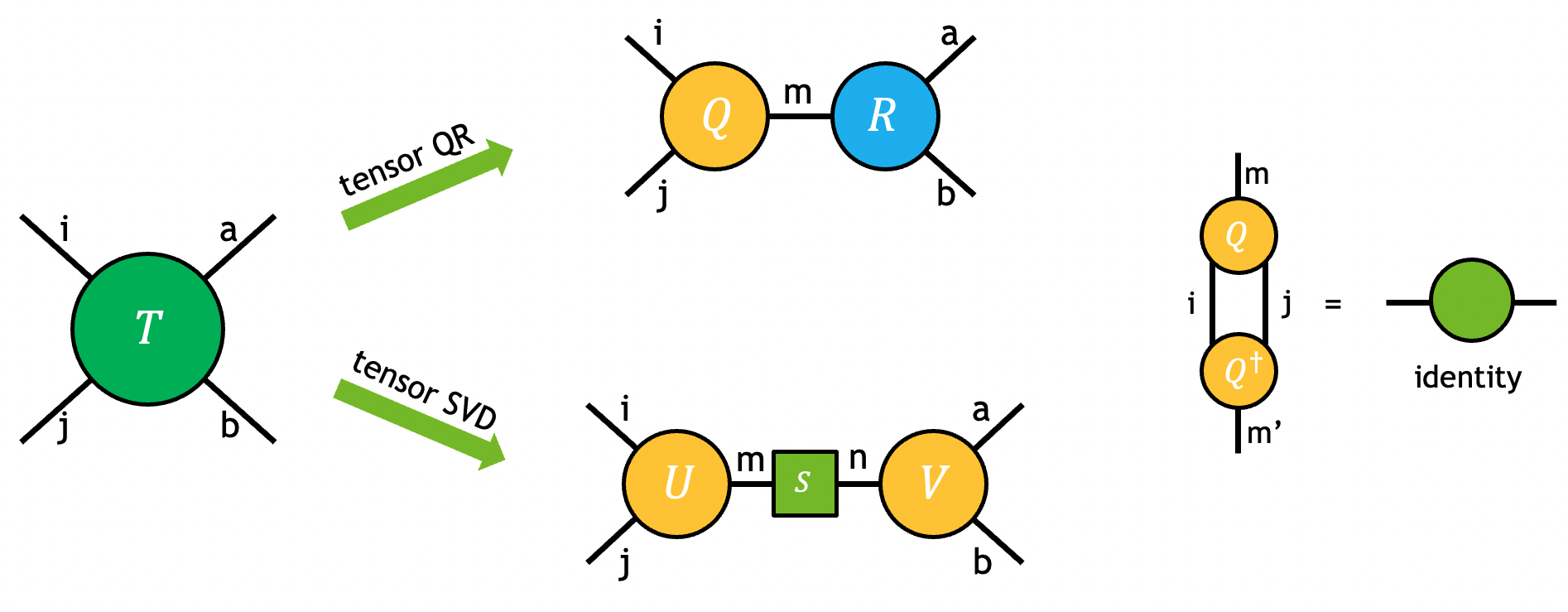
虽然张量网络收缩路径优化可以大大降低张量网络精确收缩的计算成本，但随着网络规模和复杂性的增加，成本仍然可能迅速扩展到经典计算机的极限之外。已经开发了各种近似张量网络方法来应对这一挑战，例如基于矩阵乘积态 (MPS) 的算法。这些方法通常旨在利用张量网络中的稀疏性，使用张量分解技术，如 QR 和 SVD。

张量的 QR 和 SVD 分解可以通过下图可视化，并且可以看作是矩阵 QR/SVD 的高阶推广。

../_images/tensor_decomp.png

问题可以由用户请求的输出张量中模式的划分完全指定。例如，上图中的张量 \(T\) 使用张量 SVD 分解为输出张量 \(U\)、\(S\) 和 \(V\)

\[T_{iajb} = U_{ijm} S_{mn} V_{ban}\]

注意

虽然输出 \(S\) 在方程和图中表示为矩阵，但只有其对角元素是非零的。在 cuTensorNet 的所有 SVD 相关 API 中，仅返回非零对角元素（作为向量）。

一旦确定了 \(U\) 和 \(V\) 中模式的划分，首先将输入张量 \(T\) 置换为中间张量 \(\bar{T}\)，并具有正确的模式顺序，以便可以将其视为分解的矩阵

\[T_{iajb} \rightarrow \text{permute} \rightarrow \bar{T}_{ijba} \rightarrow \text{SVD} \rightarrow \bar{U}_{ijm}S_{mn}\bar{V}_{nba}\]

在矩阵 SVD/QR 分解之后，可能仍然需要置换来变换输出中间张量 \(\bar{U}\) 和 \(\bar{V}\)，以获得请求的输出 \(U\) 和 \(V\)。

注意

cuTensorNet 中的张量 SVD 和 QR 以简化模式运行，即 \(k=min(m, n)\)，其中 k 表示输出共享模式的范围，而 m 和 n 表示有效输入矩阵的行/列大小。 虽然张量 QR 始终是精确的，但 cuTensorNet 提供了不同的方法供用户截断奇异值、\(\bar{U}\) 和 \(\bar{V}\)。 例如，如果用户希望在张量 SVD 中执行固定范围截断，则可以将 \(k\) 设置为低于 \(min(m, n)\)。 有关详细说明，请参阅 SVD 选项。

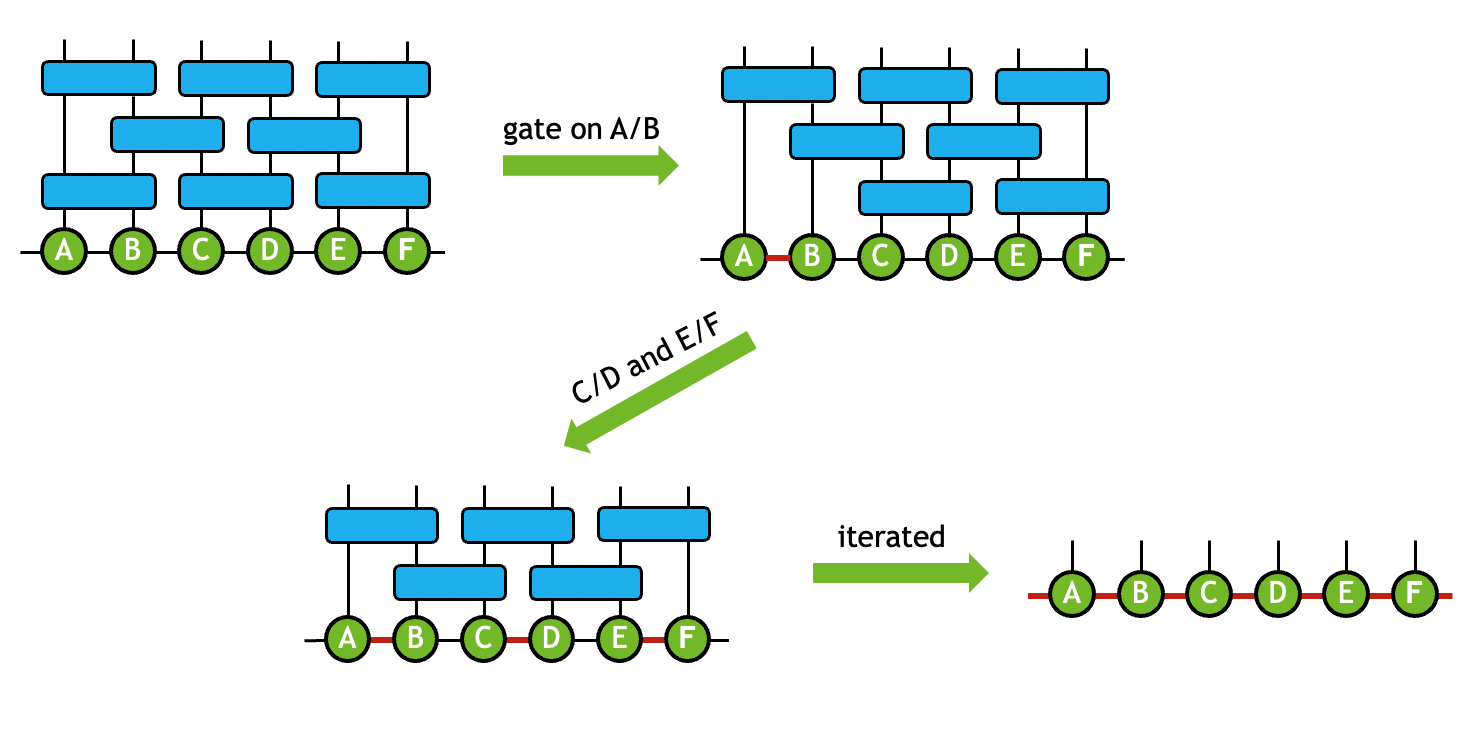
在实践中，张量分解和成对张量收缩通常结合在一起，以将原始网络转换为新的拓扑结构，从而反映其在量子模拟领域的内部稀疏性或纠缠几何结构。 例如，在矩阵乘积态 (MPS) 模拟器中，量子比特状态被映射到一维张量链。 当门张量应用于 MPS 时，会执行一系列收缩和张量 QR/SVD 运算，以确保输出状态仍然表示为一维张量链。 用于维护 MPS 几何结构的复合运算称为门分割过程。 例如，一个双量子比特门张量 \(G\) 应用于两个连接张量 \(A\) 和 \(B\)，以生成具有与 \(A\) 和 \(B\) 相似模式的输出张量 \(\tilde{A}\) 和 \(\tilde{B}\)

\[A_{ipj} B_{jql} G_{pqrs} \rightarrow \text{gate split} \rightarrow \tilde{A}_{irx}\tilde{B}_{jsl}\]

在门分割过程中，奇异值的数量也可能被截断，以保持 MPS 大小可处理。 通过在整个网络中迭代此过程，原始张量网络可以由输出 MPS 状态近似表示。 该过程可以图解如下

../_images/gate_split.png

有关如何执行变换的更详细说明，请参阅下面的 门分割算法。

收缩优化器

收缩路径是以 numpy.einsum_path() 格式表示的一系列成对收缩。 对于给定的张量网络，收缩成本可能相差几个数量级，具体取决于收缩路径的质量。 因此，至关重要的是使用路径优化器来找到使张量网络收缩的总成本最小化的收缩路径。 目前，收缩成本指的是 cuTensorNet 路径优化器目的的浮点运算次数 (FLOP)，而最佳收缩路径对应于 FLOP 计数最小的路径。

cuTensorNet 路径优化器基于图划分方法（称为第 1 阶段），然后是交错切片和重构优化（称为第 2 阶段）。 实际上，经验表明，找到最佳收缩路径可能对配置参数的选择很敏感，这些参数可以通过 cutensornetContractionOptimizerConfigSetAttribute() 进行配置，并通过 cutensornetContractionOptimizerConfigGetAttribute() 进行查询。 本节的其余部分旨在介绍整体优化方案和这些可配置参数。

优化完成后，它会返回一个不透明对象 cutensornetContractionOptimizerInfo_t，其中包含用于创建收缩计划的所有属性。 例如，最佳路径（CUTENSORNET_CONTRACTION_OPTIMIZER_INFO_PATH）和相应的 FLOP 计数（CUTENSORNET_CONTRACTION_OPTIMIZER_INFO_FLOP_COUNT）可以通过 cutensornetContractionOptimizerInfoGetAttribute() 查询。

注意

返回的 FLOP 计数假设输入张量是实数值的； 对于复数值张量，将其乘以 4 是一个很好的估计。

或者，我们可以完全绕过 cuTensorNet 优化器，通过使用 cutensornetContractionOptimizerInfoSetAttribute() 提供您自己的路径。 对于未设置的 cutensornetContractionOptimizerInfo_t 属性（例如：切片数和 FLOP），cuTensorNet 将使用默认值或在适用时动态计算它们。

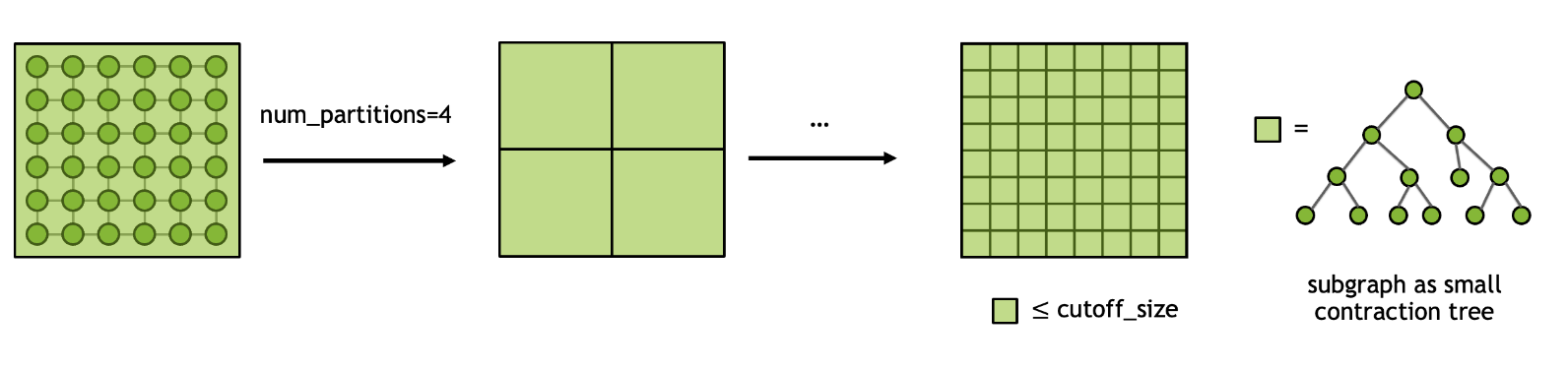
图划分

一般来说，为给定的张量网络搜索最佳收缩路径是一个 NP 难题。 因此，至关重要的是以分而治之的精神来处理这个问题。 给定一个输入张量网络，我们首先执行图划分以将网络拆分为 N 个较小的子图，并递归重复此过程，直到每个子图的大小小于截止大小。 一旦确定了最终的划分方案，找到首先在每个子图中收缩，然后收缩所有子图的路径就变得容易处理。 该过程可以使用下图说明，我们得到了一个粗略的收缩路径或收缩树，用于后续优化。

../_images/graph_partition.png

cuTensorNet 库通过以下参数提供对图划分算法的控制

切片

为了使张量网络收缩适应可用的设备内存（如 workspaceSizeConstraint 所指定），可能需要使用切片（也称为变分投影或键切割）。 通过切片，我们将整个张量网络的收缩拆分为多个独立的较小收缩，其中每个收缩仅考虑特定模式（或模式组合）的特定位置。 创建的切片总数等于切片模式的范围的乘积。 可以通过对每个切片收缩的输出求和来获得完整张量网络收缩的结果。 以上面的张量 \(T\) 为例，如果我们对模式 i 进行切片，我们将获得以下表示

\[T_{abcd} = A_{aij} B_{bjk} C_{klc} D_{lid} \longrightarrow \sum_{i_s} \left( A_{a {i_s} j} B_{bjk} C_{klc} D_{l {i_s} d} \right),\]
../_images/slicing.png

正如从图中可以看到的，切片模式 \(i_s\) 不再作为张量收缩的一部分隐式求和，而是在最后一步中显式求和。 因此，切片可以有效地减少收缩大型张量网络（特别是量子电路）的内存占用。 此外，由于每个切片收缩都与其他切片收缩无关，因此可以在各种分布式设置中有效地并行化计算。

尽管有上述所有优点，但切片的缺点是它通常会增加整个收缩的总 FLOP 计数。 切片的开销很大程度上取决于收缩路径和切片的模式。 一般来说，没有简单的方法来确定最佳的切片模式集。

cuTensorNet 库中的切片查找算法可以通过以下参数进行调整

cuTensorNet 库中的切片查找算法利用了一组启发式方法，并且该过程可以与 subtree 重构 例程耦合，以找到既满足内存约束又产生最小开销的最佳模式集。

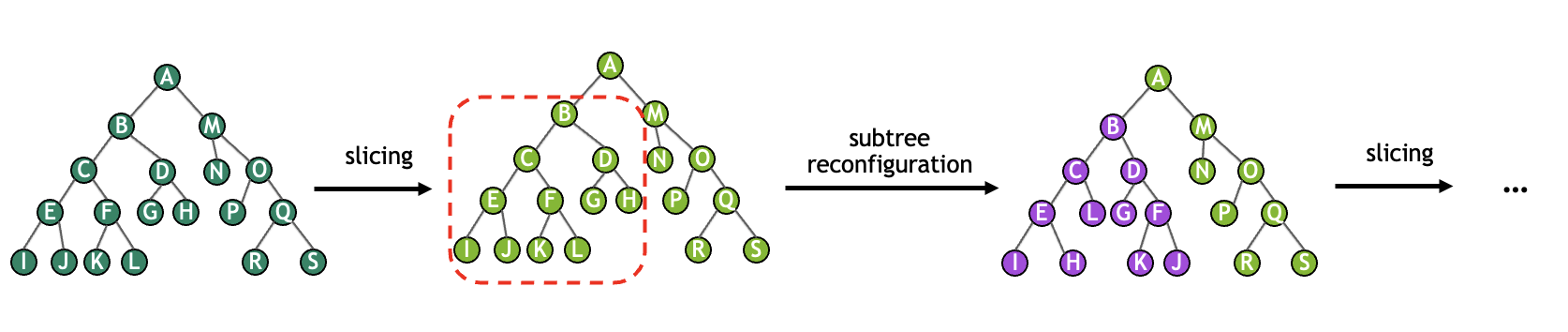
重构

在每次切片查找迭代结束时，收缩树的质量会因切片而降低。 我们可以通过执行重构来改进此阶段的收缩树。 重构考虑了完整收缩树中的多个小子树，并尝试提高其质量。 切片和重构的重复过程可以如下图所示。

../_images/subtree_reconfiguration.png

虽然此过程在计算上是昂贵的，但没有重构的切片收缩树的执行成本可能比预期的要高几个数量级。 cuTensorNet 库提供了一些控件来影响重构算法

  • CUTENSORNET_CONTRACTION_OPTIMIZER_CONFIG_RECONFIG_NUM_ITERATIONS：指定每次重构期间要考虑的子树数量。 重构中花费的时间（通常占优化器运行时间的大部分）与此值成线性比例。 根据我们的实验，介于 500 和 1000 之间的值提供了非常好的结果。 默认为 500。 将此值设置为 0 将禁用重构。

  • CUTENSORNET_CONTRACTION_OPTIMIZER_CONFIG_RECONFIG_NUM_LEAVES：指定重构考虑的每个子树中的最大叶节点数。 由于对于最佳子树重构，所花费的时间在此数量上呈指数增长，因此选择较大的值将调用更快的非最佳算法。 尽管如此，随着此数量的增加，重构所花费的时间会非常迅速地增加。 默认为 8。 必须至少为 2。 虽然使用默认值通常会产生最佳 FLOP 计数，但在许多问题中，将其设置为 6 将加快优化器执行速度，而不会显着增加 FLOP 计数。

延迟秩简化

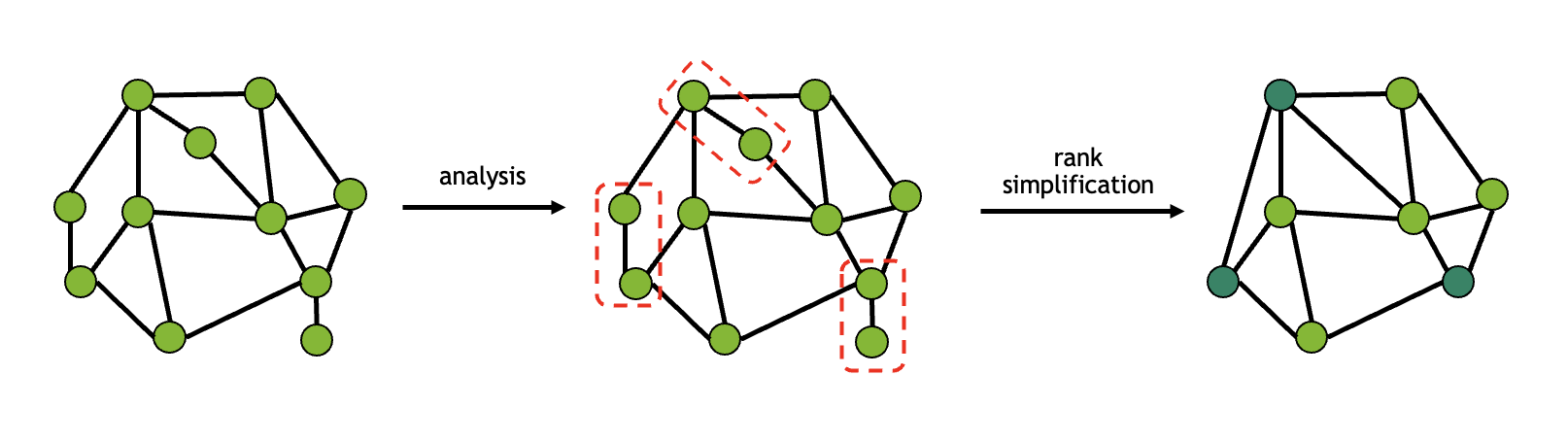
由于路径查找算法所花费的时间随着张量数量的增加而迅速增加，因此尽可能减少张量数量是有利的。 秩简化从网络中删除不重要的张量收缩，以提高性能。 这些收缩是指张量仅与最多两个邻居连接的收缩，有效地使收缩成为小的矩阵-向量或矩阵-矩阵乘法。 下图给出了秩简化的一个示例

../_images/rank_simplification.png

此技术对于低连通性的张量网络特别有用； 例如，量子电路中的所有单量子比特门都可以与相邻的多量子比特门融合，从而减少优化器的搜索空间。 执行简化所需的收缩不会立即执行，而是预先添加到返回的收缩路径中。 如果出于某种原因不希望进行这种简化，则可以禁用它

虽然简化在大多数情况下有助于降低 FLOP 计数，但在某些情况下（取决于网络拓扑和其他因素），它可能会导致具有更高 FLOP 计数的路径。 我们建议用户试验关闭简化（使用上面列出的选项）对计算路径的影响。

超优化器

cuTensorNet 为路径优化提供了一个超优化器，它可以自动生成多个收缩路径实例，并返回其中总 FLOP 计数最佳的实例。 实例数量由用户通过使用 CUTENSORNET_CONTRACTION_OPTIMIZER_CONFIG_HYPER_NUM_SAMPLES 来控制，默认设置为 0。 这里的想法是，超优化器将创建 CUTENSORNET_CONTRACTION_OPTIMIZER_CONFIG_HYPER_NUM_SAMPLES 个实例，每个实例都反映了优化器算法中不同参数的使用。 每个实例将运行完整的优化器算法，包括重构和切片（如果请求）。 在超优化器循环结束时，将返回最佳路径（就 FLOP 计数而言）。

超优化器并行运行其实例。 所需的线程数可以使用 CUTENSORNET_CONTRACTION_OPTIMIZER_CONFIG_HYPER_NUM_THREADS 设置，默认情况下选择可用逻辑核心数的一半。 线程数限制为可用逻辑核心数，以避免线程数较多时可能发生的资源争用。

在内部，cuTensorNet 为超优化器等中的多线程处理保留了一个线程池。 线程池生命周期绑定到 cuTensorNet 句柄。 （在以前的版本中，使用了 OpenMP；自 cuTensorNet v2.0.0 以来，情况已不再如此。）

超优化器更改的配置参数可以在 图划分 部分中找到。 其中一些参数可以固定为给定值（通过 cutensornetContractionOptimizerConfigSetAttribute()）。 当参数固定时，超优化器将不会随机化它。 随机性可以通过使用属性 CUTENSORNET_CONTRACTION_OPTIMIZER_CONFIG_SEED 设置种子来固定。

中间张量重用

cuTensorNet 当前支持中间张量的缓存/重用，以用于某些输入张量的值发生变化，但网络结构不变的情况。 在这种情况下，它可以显着加速同一张量网络的重复执行，其中某些张量更新其值。 一个例子是计算单个位串或小批量位串的概率幅度，该过程通常用于量子处理器的验证/确认。 在这种情况下，只有第一个位串幅度的计算会产生完整的计算成本，而后续位串概率幅度的计算应该运行得更快，并受益于中间张量缓存/重用。 另一个例子是最终量子电路状态的概率分布的采样。 采样过程也将受益于中间重用，因为为量子比特组计算的基础约化密度矩阵不会改变其结构，而只会更新相对少量的输入张量的值。 最后，具有相对少量变分参数的变分量子算法也可以通过这项新功能加速。

要为常量输入张量激活中间张量重用，用户需要

近似设置

SVD 选项

除了上面提到的标准张量 SVD 之外，cuTensorNet 还允许用户在使用各种 SVD 算法进行分解期间执行截断、归一化和重分区。对于截断，最常见的策略是保留最大的 k 个奇异值并裁剪掉剩余的奇异值。在 cuTensorNet 中，这可以通过修改输出 cutensornetTensorDescriptor_t 对象中共享模式的范围来轻松指定。或者，用户可以在运行时基于实际值或特征值的分布来截断奇异值。这种截断设置、SVD 算法以及归一化和重分区选项由 cutensornetTensorSVDConfig_t 对象的不同属性提供。

注意

cutensornetTensorSVDConfig_t 中基于值的截断选项可以与固定维度截断结合使用，但由于在运行时找到的实际缩减维度是未知的，因此输出张量的数据分配大小应始终基于没有基于值的截断的假设。执行后，运行时找到的可能缩减的维度将存储在 CUTENSORNET_TENSOR_SVD_INFO_REDUCED_EXTENT 的 cutensornetTensorSVDInfo_t 属性中，并且也反映在输出 cutensornetTensorDescriptor_t 中。用户可以调用 cutensornetTensorSVDInfoGetAttribute() 或 cutensornetGetTensorDetails() 来查询此信息。

门分裂算法

一般来说，执行门分裂操作的方法不止一种。cuTensorNet 在 cutensornetGateSplitAlgo_t 中为此目的提供了两种算法

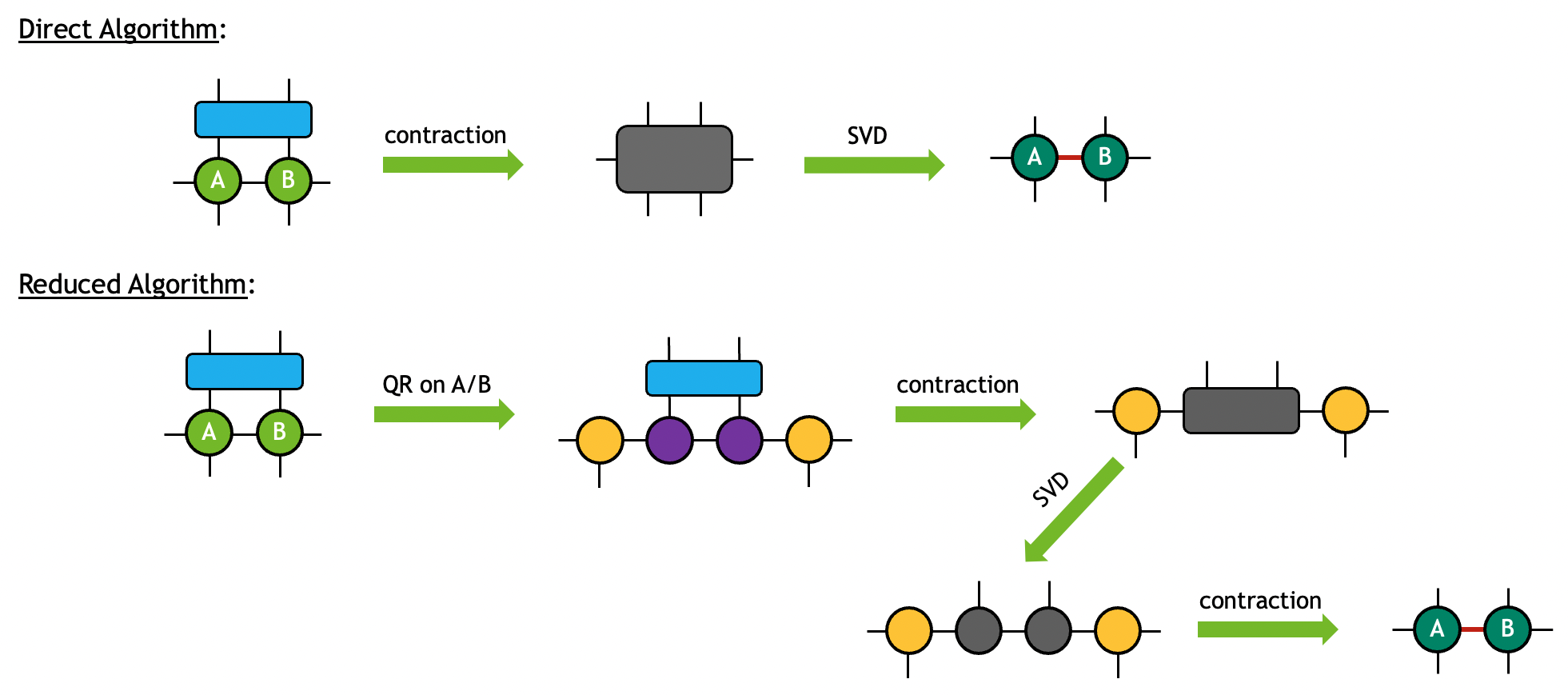
  • CUTENSORNET_GATE_SPLIT_ALGO_DIRECT: 三个输入张量将首先被缩并以形成中间张量。随后将进行张量 SVD，以将中间张量分解为所需的输出。当张量尺寸相对较小时，此算法通常更占用内存，但性能更高。

  • CUTENSORNET_GATE_SPLIT_ALGO_REDUCED: 输入张量 A 和 B 将首先通过张量 QR 分解分解为更小的片段。分解中的两个 R 张量将随后与输入张量 G 缩并以形成中间张量。随后将进行张量 SVD 以分解中间张量，其输出将随后与第一步中的 Q 张量缩并以形成所需的输出。当张量尺寸变大时，此算法通常占用内存更少且性能更高。

注意

对于 CUTENSORNET_GATE_SPLIT_ALGO_REDUCED, 如果在分解中无法实现内存大小缩减，cuTensorNet 可能会在内部跳过张量 A 或/和 B 上的 QR 分解。

这两种算法可以图表形式可视化如下（在此示例中，奇异值被平均分配到两个输出上）

../_images/gate_split_algo.png

支持的数据类型

对于张量网络缩并，数据和计算类型的有效组合以直接的方式继承自 cuTENSOR。有关详细信息，请参考 cutensornetCreateNetworkDescriptor() 和 cuTENSOR 的用户指南。

对于近似张量网络功能，包括张量 SVD/QR 分解和门分裂操作，支持以下数据类型

注意

对于门分裂操作，上述数据类型的有效计算类型与张量网络缩并的计算类型一致。

参考文献

有关 cuTensorNet 的技术介绍，请参考 NVIDIA 博客

有关通用张量网络的更多信息，请参考以下内容

有关张量网络在量子电路模拟中的应用，请参阅

引用 cuQuantum

    1. Bayraktar et al., “cuQuantum SDK: A High-Performance Library for Accelerating Quantum Science,” 2023 IEEE International Conference on Quantum Computing and Engineering (QCE), Bellevue, WA, USA, 2023, pp. 1050-1061, doi: 10.1109/QCE57702.2023.00119.