使用 FP8 与 Transformer Engine

H100 GPU 引入了对新数据类型 FP8（8 位浮点）的支持，从而实现了更高的矩阵乘法和卷积吞吐量。在本例中，我们将介绍 FP8 数据类型，并展示如何将其与 Transformer Engine 一起使用。

FP8 简介

结构

H100 支持的 FP8 数据类型实际上是 2 种不同的数据类型，在神经网络的训练的不同部分很有用

  • E4M3 - 它由 1 个符号位、4 个指数位和 3 个尾数位组成。它可以存储高达 +/-448 的值和 nan。

  • E5M2 - 它由 1 个符号位、5 个指数位和 2 个尾数位组成。它可以存储高达 +/-57344、+/- inf 和 nan 的值。动态范围增加的代价是存储值的精度降低。

c819d75333144e6891e28b9ae2f9f119

图 1：浮点数据类型的结构。所有显示的值（在 FP16、BF16、FP8 E4M3 和 FP8 E5M2 中）都是值 0.3952 的最接近表示。

在训练神经网络期间，可以使用这两种类型。通常，前向激活和权重需要更高的精度，因此 E4M3 数据类型最适合在前向传播期间使用。然而，在反向传播中，流经网络的梯度通常不太容易受到精度损失的影响，但需要更高的动态范围。因此，最好使用 E5M2 数据格式存储它们。H100 TensorCore 提供对这些类型的任意组合作为输入的支持，使我们能够使用其首选精度存储每个张量。

混合精度训练 - 快速入门

为了理解如何将 FP8 用于训练深度学习模型，首先回顾一下混合精度如何与其他数据类型（尤其是 FP16）一起工作是很有用的。

FP16 训练的混合精度配方有两个组成部分：选择哪些操作应以 FP16 精度执行以及动态损失缩放。

  • 选择以 FP16 精度执行的操作需要分析操作输出相对于输入的数值行为以及预期的性能优势。这使得可以将矩阵乘法、卷积和归一化层等操作标记为安全，同时将需要高精度的 norm 或 exp 操作保留。

  • 动态损失缩放能够避免训练期间梯度的上溢和下溢。这些情况可能会发生，因为虽然 FP16 的动态范围足以存储梯度值的分布，但此分布可能以对于 FP16 来说过高或过低的值为中心。缩放损失会将这些分布（通过仅使用 2 的幂而不影响数值）转移到 FP16 中可表示的范围内。

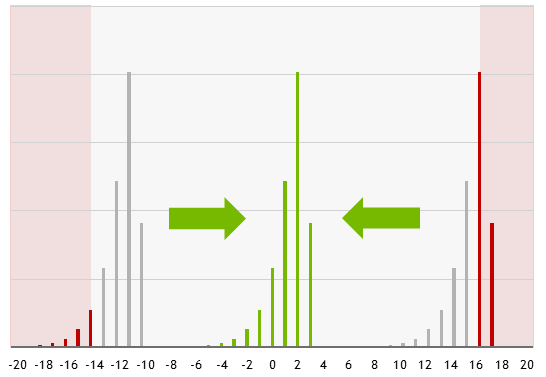
821e7d1b9b1a4ee4a6f50d65a29decec

图 2：缩放损失使梯度分布能够转移到 FP16 数据类型的可表示范围内。

使用 FP8 进行混合精度训练

虽然 FP8 类型提供的动态范围足以存储任何特定的激活或梯度，但不足以同时存储所有这些。这使得对 FP16 有效的单个损失缩放因子策略对于 FP8 训练不可行，而是需要为每个 FP8 张量使用不同的缩放因子。

有多种策略可用于为给定的 FP8 张量选择合适的缩放因子

  • 即时缩放。此策略基于正在生成的张量的绝对值最大值 (amax) 选择缩放因子。在实践中，这是不可行的，因为它需要多次遍历数据 - 运算符以更高的精度生成和写出输出，然后找到输出的绝对值最大值并应用于所有值，以便获得最终的 FP8 输出。这导致了大量的开销，严重削弱了使用 FP8 带来的增益。

  • 延迟缩放。此策略基于在之前若干次迭代中看到的绝对值最大值来选择缩放因子。这使得 FP8 计算能够充分发挥性能，但需要将最大值历史记录存储为 FP8 运算符的附加参数。

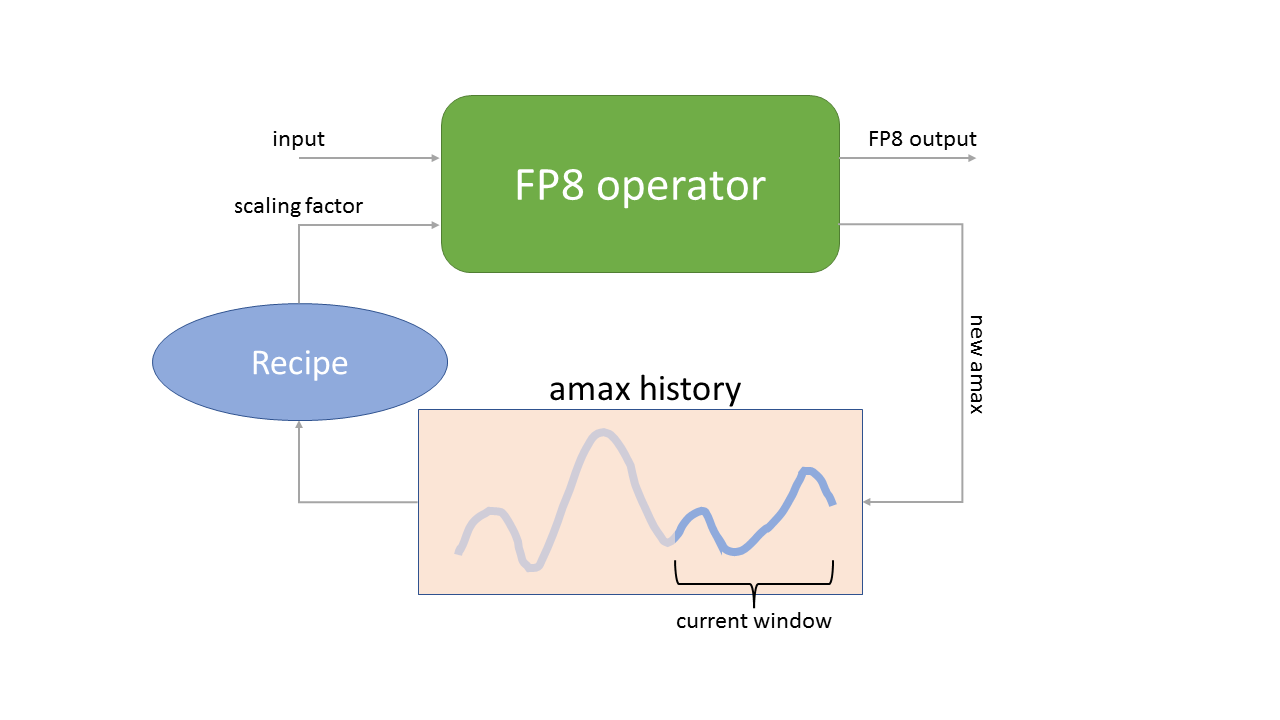
543a86eee0e8436eacacbd3ba495d203

图 3：延迟缩放策略。FP8 运算符使用通过在之前若干次迭代中看到的 amaxes（绝对值最大值）历史记录获得的缩放因子，并生成 FP8 输出和当前 amax，后者存储在历史记录中。

正如在图 3 中可以看到的，延迟缩放策略既需要存储 amaxes 的历史记录，还需要选择一种将该历史记录转换为下一次迭代中使用的缩放因子的配方。

MXFP8 和块缩放

NVIDIA Blackwell 架构引入了对 FP8 格式的新变体：MXFP8 的支持。

MXFP8 vs FP8

“常规” FP8 和 MXFP8 之间的主要区别在于缩放的粒度。在 FP8 中，每个张量都有一个 FP32 缩放因子，因此张量中的所有值都需要“适合” FP8 数据类型的动态范围内。这需要使用精度较低的 E5M2 格式来表示网络中的某些张量（如梯度）。

MXFP8 通过为每 32 个连续值的块分配不同的缩放因子来解决此问题。这允许使用 E4M3 数据类型表示所有值。

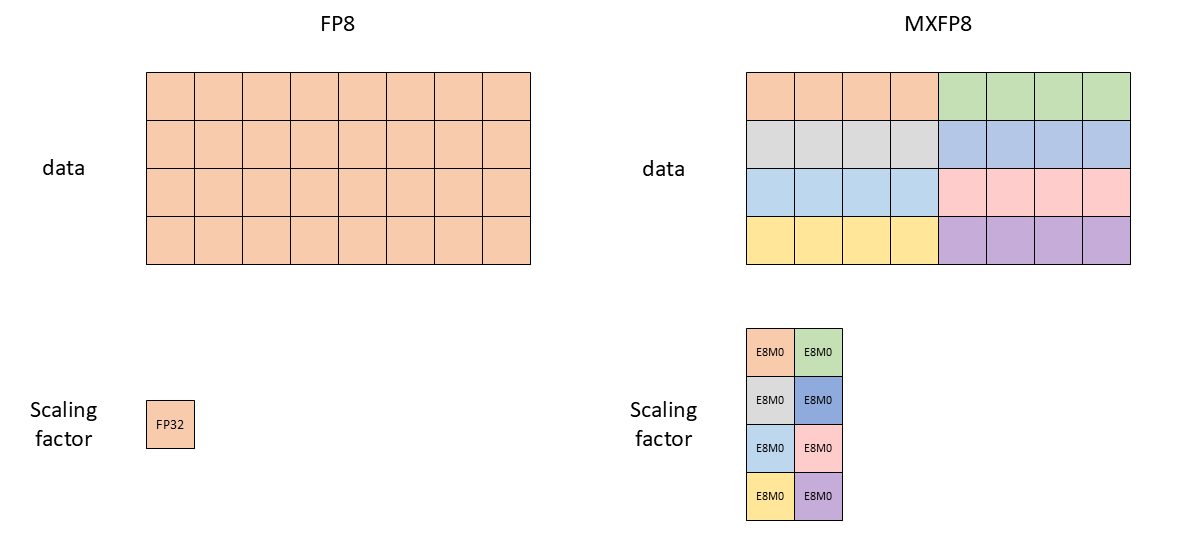
f9a78e7e2e6f4902a232a4cbb3b1383d

图 4：MXFP8 对单个张量使用多个缩放因子。为了简单起见，图片仅显示每个块 4 个值，但实际的 MXFP8 每个块有 32 个值。

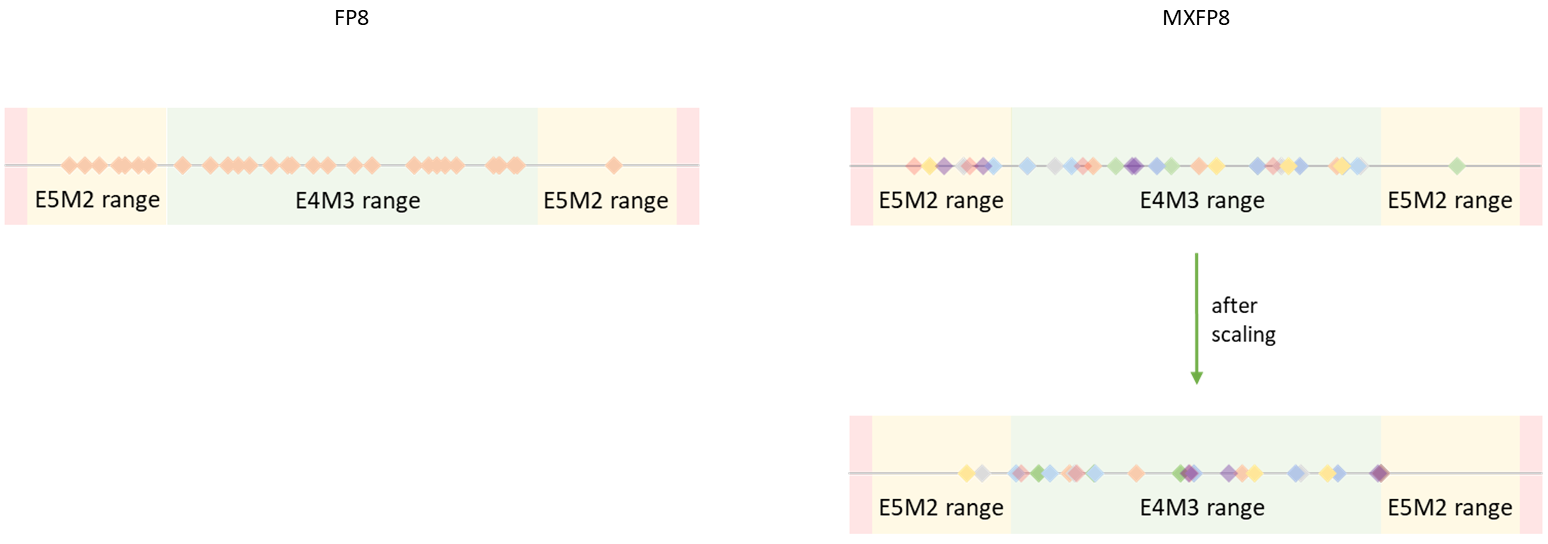
8332c6d54b554de1b01ac1e69befd26a

图 5：由于有多个缩放因子，张量的动态范围要求降低，因此可以使用 E4M3 格式，因为饱和为 0 的元素要少得多。

第二个区别是用于存储缩放因子数据类型。FP8 使用 FP32 (E8M23)，而 MXFP8 使用 8 位 2 的幂表示 (E8M0)。

765d85fc805a46e7a42afa1f3607df55

图 6：用于在 MXFP8 中存储缩放因子的 E8M0 数据类型的结构。

处理转置

线性层的前向和反向传播涉及具有不同缩减维度的多个矩阵乘法。Blackwell Tensor Core 要求 MXFP8 数据在缩减维度上是“连续的”，因此 MXFP8 训练在不同点使用非转置和转置的 MXFP8 张量。然而，虽然转置 FP8 数据在数值上是微不足道的，但转置 MXFP8 数据需要重新量化。

为了避免与这种双重量化相关的精度损失，Transformer Engine 从原始高精度输入创建张量的常规副本和转置副本。

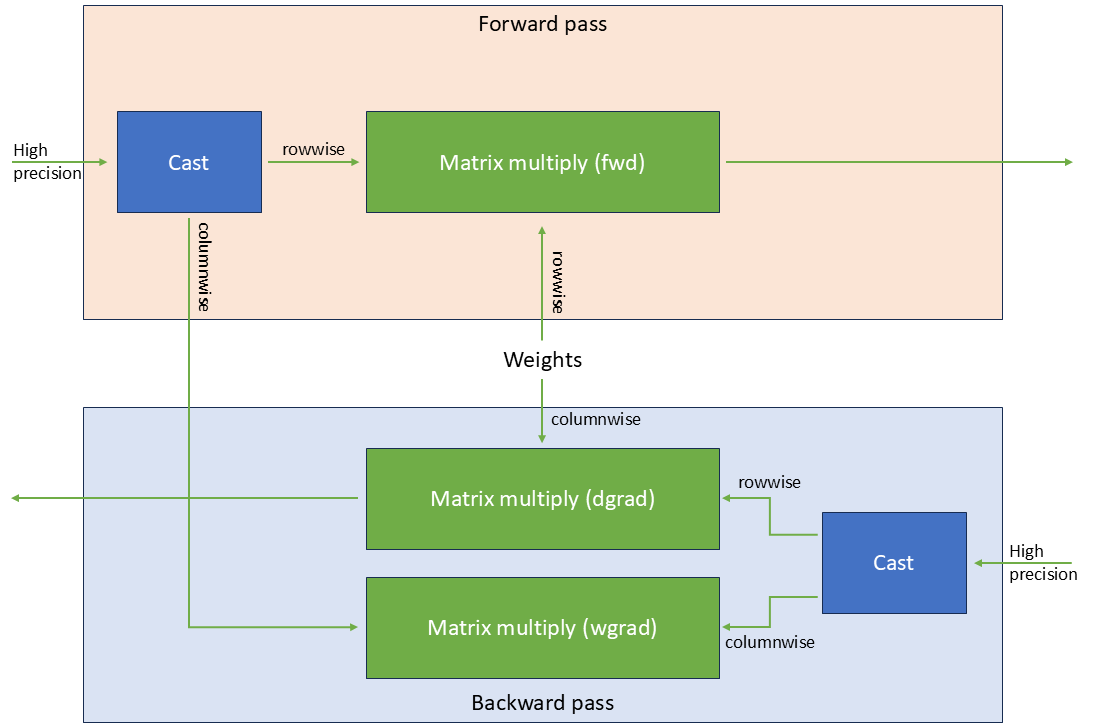
5d5d83b4d5b94f39a3d394061ffb3534

图 7：MXFP8 中的线性层。计算前向和反向传播都需要在两个方向上量化的张量。

将 FP8 与 Transformer Engine 结合使用

Transformer Engine 库提供了工具，可以使用 FP8 延迟缩放和 MXFP8 策略轻松进行 FP8 数据类型训练。

FP8 配方

DelayedScaling 配方来自 transformer_engine.common.recipe 模块，存储了使用 FP8 延迟缩放进行训练所需的所有选项：用于缩放因子计算的 amax 历史记录的长度、FP8 数据格式等。类似地，来自同一模块的 MXFP8BlockScaling 可用于启用 MXFP8 训练。

[1]:

from transformer_engine.common.recipe import Format, DelayedScaling, MXFP8BlockScaling

fp8_format = Format.HYBRID  # E4M3 during forward pass, E5M2 during backward pass
fp8_recipe = DelayedScaling(fp8_format=fp8_format, amax_history_len=16, amax_compute_algo="max")
mxfp8_format = Format.E4M3  # E4M3 used everywhere
mxfp8_recipe = MXFP8BlockScaling(fp8_format=mxfp8_format)

然后，此配方用于配置 FP8 训练。

FP8 自动类型转换

并非每个操作都适合使用 FP8 执行。Transformer Engine 库提供的所有模块都旨在从 FP8 数据类型中提供最大性能优势，同时保持精度。为了启用 FP8 操作，TE 模块需要包装在 fp8_autocast 上下文管理器中。

[2]:

import transformer_engine.pytorch as te
import torch

torch.manual_seed(12345)

my_linear = te.Linear(768, 768, bias=True)

inp = torch.rand((1024, 768)).cuda()

with te.fp8_autocast(enabled=True, fp8_recipe=fp8_recipe):
    out_fp8 = my_linear(inp)

fp8_autocast 上下文管理器隐藏了处理 FP8 的复杂性

  • 所有 FP8 安全操作的输入都转换为 FP8

  • Amax 历史记录已更新

  • 新的缩放因子已计算完成，并为下一次迭代做好准备

注意

Transformer Engine 的 Linear 层中对 FP8 的支持目前仅限于形状的张量，其中两个维度都可以被 16 整除。就完整 Transformer 网络的输入而言，这通常需要将序列长度填充为 16 的倍数。

处理反向传播

当模型在 fp8_autocast 区域内运行时，尤其是在多 GPU 训练中，需要进行一些通信以同步缩放因子和 amax 历史记录。为了在不引入太多开销的情况下执行该通信，fp8_autocast 上下文管理器在执行通信之前聚合张量。

由于这种聚合，反向调用需要在 fp8_autocast 上下文管理器外部发生。它对计算精度没有影响 - 反向传播的精度由前向传播的精度决定。

[3]:

loss_fp8 = out_fp8.mean()

loss_fp8.backward()  # This backward pass uses FP8, since out_fp8 was calculated inside fp8_autocast

out_fp32 = my_linear(inp)
loss_fp32 = out_fp32.mean()
loss_fp32.backward()  # This backward pass does not use FP8, since out_fp32 was calculated outside fp8_autocast

精度

如果我们比较 FP32 和 FP8 执行的结果，我们会看到它们相对接近，但有所不同

[4]:

out_fp8

[4]:

tensor([[ 0.2276,  0.2627,  0.3001,  ...,  0.0346,  0.2211,  0.1188],
        [-0.0963, -0.3725,  0.1717,  ...,  0.0901,  0.0522, -0.3472],
        [ 0.4526,  0.3482,  0.5976,  ..., -0.0687, -0.0382,  0.1566],
        ...,
        [ 0.1698,  0.6061,  0.0385,  ..., -0.2875, -0.1152, -0.0260],
        [ 0.0679,  0.2946,  0.2751,  ..., -0.2284,  0.0517, -0.1441],
        [ 0.1865,  0.2353,  0.9172,  ...,  0.1085,  0.1135,  0.1438]],
       device='cuda:0', grad_fn=<_LinearBackward>)

[5]:

out_fp32

[5]:

tensor([[ 0.2373,  0.2674,  0.2980,  ...,  0.0233,  0.2498,  0.1131],
        [-0.0767, -0.3778,  0.1862,  ...,  0.0858,  0.0676, -0.3369],
        [ 0.4615,  0.3593,  0.5813,  ..., -0.0779, -0.0349,  0.1422],
        ...,
        [ 0.1914,  0.6038,  0.0382,  ..., -0.2847, -0.0991, -0.0423],
        [ 0.0864,  0.2895,  0.2719,  ..., -0.2388,  0.0772, -0.1541],
        [ 0.2019,  0.2275,  0.9027,  ...,  0.1022,  0.1300,  0.1444]],
       device='cuda:0', grad_fn=<_LinearBackward>)

发生这种情况是因为在 FP8 情况下，输入和权重都在计算之前转换为 FP8。如果我们使用 FP8 中可表示的输入（使用在 quickstart_utils.py 中定义的函数），我们可以看到这一点，而不是原始输入

[6]:

from quickstart_utils import cast_to_representable

inp_representable = cast_to_representable(inp)
my_linear.weight.data = cast_to_representable(my_linear.weight.data)

out_fp32_representable = my_linear(inp_representable)

print(out_fp32_representable)

tensor([[ 0.2276,  0.2629,  0.3000,  ...,  0.0346,  0.2211,  0.1188],
        [-0.0963, -0.3724,  0.1717,  ...,  0.0901,  0.0522, -0.3470],
        [ 0.4526,  0.3479,  0.5976,  ..., -0.0686, -0.0382,  0.1566],
        ...,
        [ 0.1698,  0.6062,  0.0385,  ..., -0.2876, -0.1152, -0.0260],
        [ 0.0679,  0.2947,  0.2750,  ..., -0.2284,  0.0516, -0.1441],
        [ 0.1865,  0.2353,  0.9170,  ...,  0.1085,  0.1135,  0.1438]],
       device='cuda:0', grad_fn=<_LinearBackward>)

这次差异非常小

[7]:

out_fp8 - out_fp32_representable

[7]:

tensor([[ 4.9591e-05, -1.9073e-04,  9.5367e-05,  ..., -3.8147e-06,
          4.1962e-05,  2.2888e-05],
        [ 2.2888e-05, -3.4332e-05,  2.2888e-05,  ...,  2.6703e-05,
          5.3406e-05, -1.4114e-04],
        [-3.8147e-05,  2.6703e-04, -3.8147e-06,  ..., -5.7220e-05,
          4.1962e-05, -1.9073e-05],
        ...,
        [ 1.1444e-05, -7.2479e-05, -3.8147e-06,  ...,  5.3406e-05,
         -1.5259e-05,  2.2888e-05],
        [ 4.9591e-05, -9.5367e-05,  6.8665e-05,  ..., -1.5259e-05,
          7.6294e-05,  4.5776e-05],
        [-1.5259e-05, -7.6294e-06,  1.8692e-04,  ..., -3.0518e-05,
         -4.5776e-05,  7.6294e-06]], device='cuda:0', grad_fn=<SubBackward0>)

来自 FP8 执行的结果差异在训练过程中无关紧要，但最好理解它们，例如，在调试模型期间。