使用 cuSPARSE 和 cuBLAS 的不完全 LU 分解和 Cholesky 预处理迭代方法

白皮书，描述了如何使用 cuSPARSE 和 cuBLAS 库在不完全 LU 分解和 Cholesky 预处理迭代方法中实现比 CPU 快 2 倍的速度提升。

1. 引言

大型稀疏线性系统的求解是计算力学、大气建模、地球物理学、生物学、电路仿真以及计算科学和工程领域中许多其他应用中的一个重要问题。一般来说，这些线性系统可以使用直接法或预处理迭代法求解。虽然直接法通常更可靠，但它们通常具有较大的内存需求，并且在海量并行计算机平台上不能很好地扩展。

迭代方法更适合并行化，因此可以用于解决更大的问题。目前，最流行的迭代方案属于 Krylov 子空间方法族。它们包括用于非对称线性系统的双共轭梯度稳定法 (BiCGStab) 和用于对称正定 (s.p.d.) 线性系统的共轭梯度法 (CG) [2], [11]。我们将在下一节中更详细地描述这些方法。

在实践中，我们经常使用各种预处理技术来提高迭代方法的收敛性。在本白皮书中，我们重点介绍不完全 LU 分解和 Cholesky 预处理 [11]，这是最流行的预处理技术之一。它计算系数矩阵的不完全分解，并在迭代方法的每次迭代中需要求解下三角和上三角线性系统。

为了实现预处理的 BiCGStab 和 CG，我们使用了 cuSPARSE 库中实现的稀疏矩阵-向量乘法 [3], [15] 和稀疏三角求解 [8], [16]。我们指出，这些算法的底层实现利用了 CUDA 并行编程范例 [5], [9], [13]，这使我们能够探索图形处理单元 (GPU) 的计算资源。在我们的数值实验中，不完全分解在 CPU（主机）上执行，然后将得到的下三角和上三角因子传输到 GPU（设备）内存，然后再开始迭代方法。然而，不完全分解的计算也可以在 GPU 上加速。

我们指出，这些迭代方法中可用的并行性在很大程度上取决于手头系数矩阵的稀疏模式。在我们的数值实验中，使用 GPU 上的 cuSPARSE 和 cuBLAS 库，不完全 LU 分解和 Cholesky 预处理迭代方法实现的平均速度提升超过 CPU 上 MKL [17] 实现的 2 倍。例如，对于具有 0 填充 (ilu0) 的不完全 LU 分解和 Cholesky 分解的预处理迭代方法的速度提升，如图 图 1 所示，适用于来自各种应用的矩阵。这将在最后一节中更详细地描述。

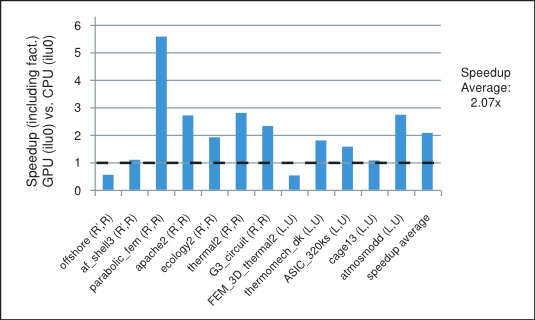
不完全 LU 分解 Cholesky（带 0 填充）预处理迭代方法的速度提升

在接下来的章节中，我们将简要描述感兴趣的方法，并评论并行稀疏矩阵-向量乘法和三角求解算法在其中所起的作用。

2. 预处理迭代方法

让我们考虑线性系统

\(A\mathbf{x} = \mathbf{f}\)

其中 \(A \in \mathbb{R}^{n \times n}\) 是非奇异系数矩阵，\(\mathbf{x},\mathbf{f} \in \mathbb{R}^{n}\) 是解向量和右端向量。

一般来说，迭代方法从初始猜测开始，并执行一系列步骤，找到更精确的解的近似值。迭代方法有两种类型：（i）平稳迭代方法，例如基于分裂的雅可比和高斯-赛德尔 (GS)，以及（ii）非平稳迭代方法，例如 Krylov 子空间方法族，其中包括 CG 和 BiCGStab。正如我们之前提到的，在本白皮书中，我们重点关注后者。

迭代方法的收敛性在很大程度上取决于系数矩阵的谱，并且可以使用预处理显着提高。预处理修改线性系统系数矩阵的谱，以减少收敛所需的迭代步数。它通常涉及找到一个预处理矩阵 \(M\)，使得 \(M^{- 1}\) 是 \(A^{- 1}\) 的良好近似，并且使用 \(M\) 的系统相对容易求解。

对于 s.p.d. 矩阵 \(A\)，我们可以让 \(M\) 为其不完全 Cholesky 分解，使得 \(A \approx M = {\widetilde{R}}^{T}\widetilde{R}\)，其中 \(\widetilde{R}\) 是上三角矩阵。 让我们假设 \(M\) 是非奇异的，那么 \({\widetilde{R}}^{- T}A{\widetilde{R}}^{- 1}\) 是 s.p.d.，并且我们可以求解预处理的线性系统而不是求解线性系统 (1)

\(\left( {{\widetilde{R}}^{- T}A{\widetilde{R}}^{- 1}} \right)\left( {\widetilde{R}\mathbf{x}} \right) = {\widetilde{R}}^{- T}\mathbf{f}\)

预处理 CG 迭代方法的伪代码如 算法 1 所示。

2.1. 算法 1 共轭梯度法 (CG)

1:	\(\text{令初始猜测为 }\mathbf{x}_{0}\text{，计算 }\mathbf{r}\leftarrow\mathbf{f} - A\mathbf{x}_{0}\)
2:	\(\textbf{for }i\leftarrow 1,2,...\text{ 直到收敛 }\textbf{do}\)
3:	\(\quad\quad\text{求解 }M\mathbf{z}\leftarrow\mathbf{r}\)	\(\vartriangleright \text{稀疏下三角和上三角求解}\)
4:	\(\quad\quad\rho_{i}\leftarrow\mathbf{r}^{T}\mathbf{z}\)
5:	\(\quad\quad\textbf{if }i==1\textbf{ then}\)
6:	\(\quad\quad\quad\quad\mathbf{p}\leftarrow\mathbf{z}\)
7:	\(\quad\quad\textbf{else}\)
8:	\(\quad\quad\quad\quad\beta\leftarrow\frac{\rho_{i}}{\rho_{i - 1}}\)
9:	\(\quad\quad\quad\quad\mathbf{p}\leftarrow\mathbf{z} + \beta\mathbf{p}\)
10:	\(\quad\quad\textbf{end if}\)
11:	\(\quad\quad\text{计算 }\mathbf{q}\leftarrow A\mathbf{p}\)	\(\vartriangleright \text{稀疏矩阵-向量乘法}\)
12:	\(\quad\quad\alpha\leftarrow\frac{\rho_{i}}{\mathbf{p}^{T}\mathbf{q}}\)
13:	\(\quad\quad\mathbf{x}\leftarrow\mathbf{x} + \alpha\mathbf{p}\)
14:	\(\quad\quad\mathbf{r}\leftarrow\mathbf{r} - \alpha\mathbf{q}\)
15:	\(\textbf{end for}\)

请注意，在不完全 Cholesky 预处理 CG 迭代方法的每次迭代中，我们需要执行一次稀疏矩阵-向量乘法和两次三角求解。下面显示了使用 C 编程语言的 cuSPARSE 和 cuBLAS 库的相应 CG 代码。

/***** CG Code *****/
/* ASSUMPTIONS:
   1. The cuSPARSE and cuBLAS libraries have been initialized.
   2. The appropriate memory has been allocated and set to zero.
   3. The matrix A (valA, csrRowPtrA, csrColIndA) and the incomplete-
      Cholesky upper triangular factor R (valR, csrRowPtrR, csrColIndR)
      have been computed and are present in the device (GPU) memory. */

//create the info and analyse the lower and upper triangular factors
cusparseCreateSolveAnalysisInfo(&inforRt);
cusparseCreateSolveAnalysisInfo(&inforR);
cusparseDcsrsv_analysis(handle,CUSPARSE_OPERATION_TRANSPOSE,
                      n, descrR, valR, csrRowPtrR, csrColIndR, inforRt);
cusparseDcsrsv_analysis(handle,CUSPARSE_OPERATION_NON_TRANSPOSE,
                      n, descrR, valR, csrRowPtrR, csrColIndR, inforR);

//1: compute initial residual r = f -  A x0 (using initial guess in x)
cusparseDcsrmv(handle, CUSPARSE_OPERATION_NON_TRANSPOSE, n, n, 1.0,
               descrA, valA, csrRowPtrA, csrColIndA, x, 0.0, r);
cublasDscal(n,-1.0, r, 1);
cublasDaxpy(n, 1.0, f, 1, r, 1);
nrmr0 = cublasDnrm2(n, r, 1);

//2: repeat until convergence (based on max. it. and relative residual)
for (i=0; i<maxit; i++){
    //3: Solve M z = r (sparse lower and upper triangular solves)
    cusparseDcsrsv_solve(handle, CUSPARSE_OPERATION_TRANSPOSE,
                         n, 1.0, descrpR, valR, csrRowPtrR, csrColIndR,
                         inforRt, r, t);
    cusparseDcsrsv_solve(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                         n, 1.0, descrpR, valR, csrRowPtrR, csrColIndR,
                         inforR, t, z);

    //4: \rho = r^{T} z
    rhop= rho;
    rho = cublasDdot(n, r, 1, z, 1);
    if (i == 0){
        //6: p = z
        cublasDcopy(n, z, 1, p, 1);
    }
    else{
        //8: \beta = rho_{i} / \rho_{i-1}
        beta= rho/rhop;
        //9: p = z + \beta p
        cublasDaxpy(n, beta, p, 1, z, 1);
        cublasDcopy(n, z, 1, p, 1);
    }

    //11: Compute q = A p (sparse matrix-vector multiplication)
    cusparseDcsrmv(handle, CUSPARSE_OPERATION_NON_TRANSPOSE, n, n, 1.0,
                   descrA, valA, csrRowPtrA, csrColIndA, p, 0.0, q);

    //12: \alpha = \rho_{i} / (p^{T} q)
    temp = cublasDdot(n, p, 1, q, 1);
    alpha= rho/temp;
    //13: x = x + \alpha p
    cublasDaxpy(n, alpha, p, 1, x, 1);
    //14: r = r - \alpha q
    cublasDaxpy(n,-alpha, q, 1, r, 1);

    //check for convergence
    nrmr = cublasDnrm2(n, r, 1);
    if (nrmr/nrmr0 < tol){
        break;
    }
}

//destroy the analysis info (for lower and upper triangular factors)
cusparseDestroySolveAnalysisInfo(inforRt);
cusparseDestroySolveAnalysisInfo(inforR);

对于非对称矩阵 \(A\)，我们可以让 \(M\) 为其不完全 LU 分解，使得 \(A \nvdash M = \widetilde{L}\widetilde{U}\)，其中 \(\widetilde{L}\) 和 \(\widetilde{U}\) 分别是下三角矩阵和上三角矩阵。 让我们假设 \(M\) 是非奇异的，那么 \(M^{- 1}A\) 是非奇异的，并且我们可以求解预处理的线性系统而不是求解线性系统 (1)

\(\left( {M^{- 1}A} \right)\mathbf{x} = M^{- 1}\mathbf{f}\)

预处理 BiCGStab 迭代方法的伪代码如 算法 2 所示。

2.2. 算法 2 双共轭梯度稳定法 (BiCGStab)

1:	\(\text{令初始猜测为 }\mathbf{x}_{0}\text{，计算 }\mathbf{r}\leftarrow\mathbf{f} - A\mathbf{x}_{0}\)
2:	\(\text{设置 }\mathbf{p}\leftarrow\mathbf{r}\text{ 并选择 }\widetilde{\mathbf{r}}\text{，例如你可以设置 }\widetilde{\mathbf{r}}\leftarrow\mathbf{r}\)
3:	\(\textbf{for }i\leftarrow 1,2,...\text{ 直到收敛 }\textbf{do}\)
4:	\(\quad\quad\rho_{i}\leftarrow{\widetilde{\mathbf{r}}}^{T}\mathbf{r}\)
5:	\(\quad\quad\textbf{if }\rho_{i}==0.0\textbf{ then}\)
6:	\(\quad\quad\quad\quad\text{方法失败}\)
7:	\(\quad\quad\textbf{end if}\)
8:	\(\quad\quad\textbf{if }i > 1\textbf{ then}\)
9:	\(\quad\quad\quad\quad\textbf{if }\omega==0.0\textbf{ then}\)
10:	\(\quad\quad\quad\quad\quad\quad\text{方法失败}\)
11:	\(\quad\quad\textbf{end if}\)
12:	\(\quad\quad\quad\quad\beta\leftarrow\frac{\rho_{i}}{\rho_{i - 1}} times \frac{\alpha}{\omega}\)
13:	\(\quad\quad\quad\quad\mathbf{p}\leftarrow\mathbf{r} + \beta\left( {\mathbf{p} - \omega\mathbf{v}} \right)\)
14:	\(\quad\quad\textbf{end if}\)
15:	\(\quad\quad\text{求解 }M\hat{\mathbf{p}}\leftarrow\mathbf{p}\)	\(\vartriangleright \text{稀疏下三角和上三角求解}\)
16:	\(\quad\quad\text{计算 }\mathbf{q}\leftarrow A\hat{\mathbf{p}}\)	\(\vartriangleright \text{稀疏矩阵-向量乘法}\)
17:	\(\quad\quad\alpha\leftarrow\frac{\rho_{i}}{{\widetilde{\mathbf{r}}}^{T}\mathbf{q}}\)
18:	\(\quad\quad\mathbf{s}\leftarrow\mathbf{r} - \alpha\mathbf{q}\)
19:	\(\quad\quad\mathbf{x}\leftarrow\mathbf{x} + \alpha\hat{\mathbf{p}}\)
20:	\(\quad\quad\textbf{if }\left\| s \right\|_{2} \leq \mathit{tol}\textbf{ then}\)
21:	\(\quad\quad\quad\quad\text{方法收敛}\)
22:	\(\quad\quad\textbf{end if}\)
23:	\(\quad\quad\text{求解 }M\hat{\mathbf{s}}\leftarrow\mathbf{s}\)	\(\vartriangleright \text{稀疏下三角和上三角求解}\)
24:	\(\quad\quad\text{计算 }\mathbf{t}\leftarrow A\hat{\mathbf{s}}\)	\(\vartriangleright \text{稀疏矩阵-向量乘法}\)
25:	\(\quad\quad\omega\leftarrow\frac{\mathbf{t}^{T}\mathbf{s}}{\mathbf{t}^{T}\mathbf{t}}\)
26:	\(\quad\quad\mathbf{x}\leftarrow\mathbf{x} + \omega\hat{\mathbf{s}}\)
27:	\(\quad\quad\mathbf{r}\leftarrow\mathbf{s} - \omega\mathbf{t}\)
28:	\(\textbf{end for}\)

请注意，在不完全 LU 分解预处理 BiCGStab 迭代方法的每次迭代中，我们需要执行两次稀疏矩阵-向量乘法和四次三角求解。下面显示了使用 C 编程语言的 cuSPARSE 和 cuBLAS 库的相应 BiCGStab 代码。

/***** BiCGStab Code *****/
/* ASSUMPTIONS:
   1. The cuSPARSE and cuBLAS libraries have been initialized.
   2. The appropriate memory has been allocated and set to zero.
   3. The matrix A (valA, csrRowPtrA, csrColIndA) and the incomplete-
      LU lower L (valL, csrRowPtrL, csrColIndL)  and upper U (valU,
      csrRowPtrU, csrColIndU) triangular factors have been
      computed and are present in the device (GPU) memory. */

//create the info and analyse the lower and upper triangular factors
cusparseCreateSolveAnalysisInfo(&infoL);
cusparseCreateSolveAnalysisInfo(&infoU);
cusparseDcsrsv_analysis(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                        n, descrL, valL, csrRowPtrL, csrColIndL, infoL);
cusparseDcsrsv_analysis(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                        n, descrU, valU, csrRowPtrU, csrColIndU, infoU);

//1: compute initial residual r = b - A x0 (using initial guess in x)
cusparseDcsrmv(handle, CUSPARSE_OPERATION_NON_TRANSPOSE, n, n, 1.0,
               descrA, valA, csrRowPtrA, csrColIndA, x, 0.0, r);
cublasDscal(n,-1.0, r, 1);
cublasDaxpy(n, 1.0, f, 1, r, 1);
//2: Set p=r and \tilde{r}=r
cublasDcopy(n, r, 1, p, 1);
cublasDcopy(n, r, 1, rw,1);
nrmr0 = cublasDnrm2(n, r, 1);

//3: repeat until convergence (based on max. it. and relative residual)
for (i=0; i<maxit; i++){
    //4: \rho = \tilde{r}^{T} r
    rhop= rho;
    rho = cublasDdot(n, rw, 1, r, 1);
    if (i > 0){
        //12: \beta = (\rho_{i} / \rho_{i-1}) ( \alpha / \omega )
        beta= (rho/rhop)*(alpha/omega);
        //13: p = r + \beta (p - \omega v)
        cublasDaxpy(n,-omega,q, 1, p, 1);
        cublasDscal(n, beta, p, 1);
        cublasDaxpy(n, 1.0,  r, 1, p, 1);
    }
    //15: M \hat{p} = p (sparse lower and upper triangular solves)
    cusparseDcsrsv_solve(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                         n, 1.0, descrL, valL, csrRowPtrL, csrColIndL,
                         infoL, p, t);
    cusparseDcsrsv_solve(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                         n, 1.0, descrU, valU, csrRowPtrU, csrColIndU,
                         infoU, t, ph);

    //16: q = A \hat{p} (sparse matrix-vector multiplication)
    cusparseDcsrmv(handle, CUSPARSE_OPERATION_NON_TRANSPOSE, n, n, 1.0,
                   descrA, valA, csrRowPtrA, csrColIndA, ph, 0.0, q);

    //17: \alpha = \rho_{i} / (\tilde{r}^{T} q)
    temp = cublasDdot(n, rw, 1, q, 1);
    alpha= rho/temp;
    //18: s = r - \alpha q
    cublasDaxpy(n,-alpha, q, 1, r, 1);
    //19: x = x + \alpha \hat{p}
    cublasDaxpy(n, alpha, ph,1, x, 1);

    //20: check for convergence
    nrmr = cublasDnrm2(n, r, 1);
    if (nrmr/nrmr0 < tol){
        break;
    }

    //23: M \hat{s} = r (sparse lower and upper triangular solves)
    cusparseDcsrsv_solve(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                         n, 1.0, descrL, valL, csrRowPtrL, csrColIndL,
                         infoL, r, t);
    cusparseDcsrsv_solve(handle, CUSPARSE_OPERATION_NON_TRANSPOSE,
                         n, 1.0, descrU, valU, csrRowPtrU, csrColIndU,
                         infoU, t, s);

    //24: t = A \hat{s} (sparse matrix-vector multiplication)
    cusparseDcsrmv(handle, CUSPARSE_OPERATION_NON_TRANSPOSE, n, n, 1.0,
                   descrA, valA, csrRowPtrA, csrColIndA, s, 0.0, t);

    //25: \omega = (t^{T} s) / (t^{T} t)
    temp = cublasDdot(n, t, 1, r, 1);
    temp2= cublasDdot(n, t, 1, t, 1);
    omega= temp/temp2;
    //26: x = x + \omega \hat{s}
    cublasDaxpy(n, omega, s, 1, x, 1);
    //27: r = s - \omega t
    cublasDaxpy(n,-omega, t, 1, r, 1);

    //check for convergence
    nrmr = cublasDnrm2(n, r, 1);
    if (nrmr/nrmr0 < tol){
        break;
    }
}

//destroy the analysis info (for lower and upper triangular factors)
cusparseDestroySolveAnalysisInfo(infoL);
cusparseDestroySolveAnalysisInfo(infoU);

如图 图 2 所示，在不完全 LU 分解和 Cholesky 预处理迭代方法的每次迭代中，大部分时间都花费在稀疏矩阵-向量乘法和三角求解上。稀疏矩阵-向量乘法已在以下参考文献中进行了广泛研究 [3], [15]。稀疏三角求解不如众所周知，因此我们简要指出用于探索其中并行性的策略，并请读者参考 NVIDIA 技术报告 [8] 以获取更多详细信息。

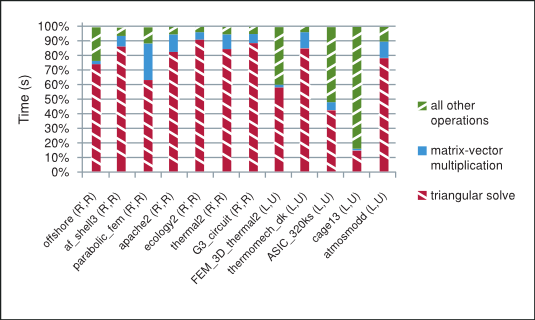
预处理迭代方法在 GPU 上花费的总时间的拆分

为了理解稀疏三角求解背后的主要思想，请注意，虽然对于稠密三角系统，正向和反向替换本质上是顺序算法，但对于稀疏三角系统，对先前获得的解元素的依赖性不一定存在。我们采用利用缺乏这些依赖性的策略，并将求解过程分成两个阶段，如 [1], [4], [6], [7], [8], [10], [12], [14] 中所述。

分析阶段构建数据依赖图，该图根据矩阵稀疏模式将独立行分组到级别中。求解阶段迭代遍历构建的级别，逐个级别并行计算与单个级别中的行对应的所有解元素。请注意，通过构造，每个级别中的行彼此独立，但依赖于前一级别中的至少一行。

分析阶段只需要执行一次，并且通常比 求解 阶段慢得多，求解 阶段可以执行多次。这种安排非常适合不完全 LU 分解和 Cholesky 预处理迭代方法。

3. 数值实验

在本节中，我们研究不完全 LU 分解和 Cholesky 预处理的 BiCGStab 和 CG 迭代方法的性能。在我们的数值实验中，我们使用了从佛罗里达大学稀疏矩阵集合 [18] 中选择的十二个矩阵。具有各自的行数 (m)、列数 (n=m) 和非零元素数 (nnz) 的七个 s.p.d. 矩阵和五个非对称矩阵被分组并按照其递增顺序显示在 表 1 中。

表 1. 对称正定 (s.p.d.) 和非对称测试矩阵

#	矩阵	m,n	nnz	s.p.d.	应用
1	offshore	259,789	4,242,673	是	地球物理学
2	af_shell3	504,855	17,562,051	是	力学
3	parabolic_fem	525,825	3,674,625	是	通用
4	apache2	715,176	4,817,870	是	力学
5	ecology2	999,999	4,995,991	是	生物学
6	thermal2	1,228,045	8,580,313	是	热模拟
7	G3_circuit	1,585,478	7,660,826	是	电路仿真
8	FEM_3D_thermal2	147,900	3,489,300	否	力学
9	thermomech_dK	204,316	2,846,228	否	力学
10	ASIC_320ks	321,671	1,316,08511	否	电路仿真
11	cage13	445,315	7,479,343	否	生物学
12	atmosmodd	1,270,432	8,814,880	否	大气模型

在以下实验中，我们使用配备 NVIDIA C2050 (ECC on) GPU 和 Intel Core i7 CPU 950 @ 3.07GHz 的硬件系统，使用 64 位 Linux 操作系统 Ubuntu 10.04 LTS、cuSPARSE 库 4.0 和 MKL 10.2.3.029。MKL_NUM_THREADS 和 MKL_DYNAMIC 环境变量保持未设置，以允许 MKL 使用最佳线程数。

我们分别使用 0 和阈值填充，使用 MKL 例程 csrilu0 和 csrilut 计算不完全 LU 分解和 Cholesky 分解。在 csrilut 例程中，我们允许三种不同的填充级别，分别用 (5,10^-3)、(10,10^-5) 和 (20,10^-7) 表示。一般来说，\(\left( k,\mathit{tol} \right)\) 填充基于 \(nnz/n + k\) 每行最大允许元素数和幅值 \(\left| l_{ij} \middle| , \middle| u_{ij} \middle| < \mathit{tol} \times \left\| \mathbf{a}_{i}^{T} \right\|_{2} \right.\) 的元素的丢弃，其中 \(l_{ij}\)、\(u_{ij}\) 和 \(\mathbf{a}_{i}^{T}\) 分别是下三角 \(L\)、上三角 \(U\) 因子和系数矩阵 \(A\) 的第 i 行的元素。

我们比较了在 GPU 上使用 cuSPARSE 和 cuBLAS 库以及在 CPU 上使用 MKL 实现的 BiCGStab 和 CG 迭代方法。在我们的实验中，我们让初始猜测为零，右端项 \(\mathbf{f} = A\mathbf{e}\)，其中 \(\mathbf{e}^{T}{= (1,\ldots,1)}^{T}\)，停止标准为最大迭代次数 2000 或相对残差 \(\left\| \mathbf{r}_{i} \right\|_{2}/\left\| \mathbf{r}_{0} \right\|_{2} < 10^{- 7}\)，其中 \(\mathbf{r}_{i} = \mathbf{f} - A\mathbf{x}_{i}\) 是第 i 次迭代的残差。

表 2. csrilu0 预处理 CG 和 BiCGStab 方法

	ilu0		CPU			GPU			速度提升
#	分解时间 (秒)	复制时间 (秒)	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	vs. ilu0
1	0.38	0.02	0.72	8.83E-08	25	1.52	8.83E-08	25	0.57
2	1.62	0.04	38.5	1.00E-07	569	33.9	9.69E-08	571	1.13
3	0.13	0.01	39.2	9.84E-08	1044	6.91	9.84E-08	1044	5.59
4	0.12	0.01	35.0	9.97E-08	713	12.8	9.97E-08	713	2.72
5	0.09	0.01	107	9.98E-08	1746	55.3	9.98E-08	1746	1.92
6	0.40	0.02	155	9.96E-08	1656	54.4	9.79E-08	1656	2.83
7	0.16	0.02	20.2	8.70E-08	183	8.61	8.22E-08	183	2.32
8	0.32	0.02	0.13	5.25E-08	4	0.52	5.25E-08	4	0.53
9	0.20	0.01	72.7	1.96E-04	2000	40.0	2.08E-04	2000	1.80
10	0.11	0.01	0.27	6.33E-08	6	0.12	6.33E-08	6	1.59
11	0.70	0.03	0.28	2.52E-08	2.5	0.15	2.52E-08	2.5	1.10
12	0.25	0.04	12.5	7.33E-08	76.5	4.30	9.69E-08	74.5	2.79

表 3. csrilut(5,10^-3) 预处理 CG 和 BiCGStab 方法

	ilut(5,10-3)		CPU			GPU			速度提升
#	分解时间 (秒)	复制时间 (秒)	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	vs. ilut (5,10-3)	vs. ilu0
1	0.14	0.01	1.17	9.70E-08	32	1.82	9.70E-08	32	0.67	0.69
2	0.51	0.03	49.1	9.89E-08	748	33.6	9.89E-08	748	1.45	1.39
3	1.47	0.02	11.7	9.72E-08	216	6.93	9.72E-08	216	1.56	1.86
4	0.17	0.01	67.9	9.96E-08	1495	26.5	9.96E-08	1495	2.56	5.27
5	0.55	0.04	59.5	9.22E-08	653	71.6	9.22E-08	653	0.83	1.08
6	3.59	0.05	47.0	9.50E-08	401	90.1	9.64E-08	401	0.54	0.92
7	1.24	0.05	23.1	8.08E-08	153	24.8	8.08E-08	153	0.93	2.77
8	0.82	0.03	0.12	3.97E-08	2	1.12	3.97E-08	2	0.48	1.10
9	0.10	0.01	54.3	5.68E-04	2000	24.5	1.58E-04	2000	2.21	1.34
10	0.12	0.01	0.16	4.89E-08	4	0.08	6.45E-08	4	1.37	1.15
11	4.99	0.07	0.36	1.40E-08	2.5	0.37	1.40E-08	2.5	0.99	6.05
12	0.32	0.03	39.2	7.05E-08	278.5	10.6	8.82E-08	270.5	3.60	8.60

数值实验的结果如 表 2 至 表 5 所示，其中我们陈述了 GPU 上的迭代方法相对于 CPU 获得的速度提升（速度提升）、收敛所需的迭代次数（# 迭代次数）、实现的相对残差 (\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)) 以及分解（fact.）、线性系统的迭代求解（solve）和下三角和上三角因子到 GPU 的 cudaMemcpy（复制）所花费的时间（秒）。我们将计算不完全 LU 分解和 Cholesky 分解以及将三角因子从 CPU 传输到 GPU 内存所花费的时间都包含在计算的速度提升中。

表 4. csrilut(10,10^-5) 预处理 CG 和 BiCGStab 方法

	ilut(10,10-5)		CPU			GPU			速度提升
#	分解时间 (秒)	复制时间 (秒)	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	vs. ilut (10,10-5)	vs. ilu0
1	0.15	0.01	1.06	8.79E-08	34	1.96	8.79E-08	34	0.57	0.63
2	0.52	0.03	60.0	9.86E-08	748	38.7	9.86E-08	748	1.54	1.70
3	3.89	0.03	9.02	9.79E-08	147	5.42	9.78E-08	147	1.38	1.83
4	1.09	0.03	34.5	9.83E-08	454	38.2	9.83E-08	454	0.91	2.76
5	3.25	0.06	26.3	9.71E-08	272	55.2	9.71E-08	272	0.51	0.53
6	11.0	0.07	44.7	9.42E-08	263	84.0	9.44E-08	263	0.59	1.02
7	5.95	0.09	8.84	8.53E-08	43	17.0	8.53E-08	43	0.64	1.68
8	2.94	0.04	0.09	2.10E-08	1.5	1.75	2.10E-08	1.5	0.64	3.54
9	0.11	0.01	53.2	4.24E-03	2000	24.4	4.92E-03	2000	2.18	1.31
10	0.12	0.01	0.16	4.89E-11	4	0.08	6.45E-11	4	1.36	1.18
11	2.89	0.09	0.44	6.10E-09	2.5	0.48	6.10E-09	2.5	1.00	33.2
12	0.36	0.03	36.6	7.05E-08	278.5	10.6	8.82E-08	270.5	3.35	8.04

表 5. csrilut(20,10^-7) 预处理 CG 和 BiCGStab 方法

	ilut(20,10-7)		CPU			GPU			速度提升
#	分解时间 (秒)	复制时间 (秒)	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	求解时间 (秒)	\(\frac{\left\| \mathbf{r}_{i} \right\|_{2}}{\left\| \mathbf{r}_{0} \right\|_{2}}\)	# 迭代次数	vs. ilut (20,10-7)	vs. ilu0
1	0.82	0.02	47.6	9.90E-08	1297	159	9.86E-08	1292	0.30	25.2
2	9.21	0.11	32.1	8.69E-08	193	84.6	8.67E-08	193	0.44	1.16
3	10.04	0.04	6.26	9.64E-08	90	4.75	9.64E-08	90	1.10	2.36
4	8.12	0.10	15.7	9.02E-08	148	22.5	9.02E-08	148	0.78	1.84
5	8.60	0.10	21.2	9.52E-08	158	53.6	9.52E-08	158	0.48	0.54
6	35.2	0.11	29.2	9.88E-08	162	80.5	9.88E-08	162	0.56	1.18
7	23.1	0.14	3.79	7.50E-08	14	12.1	7.50E-08	14	0.76	3.06
8	5.23	0.05	0.14	1.19E-09	1.5	2.37	1.19E-09	1.5	0.70	6.28
9	0.12	0.01	55.1	3.91E-03	2000	24.4	2.27E-03	2000	2.25	1.36
10	0.14	0.01	0.14	9.35E-08	3.5	0.07	7.19E-08	3.5	1.28	1.18
11	218	0.12	0.43	9.80E-08	2	0.66	9.80E-08	2	1.00
12	15.0	0.21	12.2	3.45E-08	31	4.95	3.45E-08	31	1.35	5.93

GPU 上不同不完全分解预处理的 BiCGStab 和 CG 迭代方法的性能摘要如 图 3 所示，其中 “*” 表示该方法未收敛到要求的公差。请注意，一般来说，在我们的数值实验中，随着阈值参数放宽且分解变得更稠密，不完全分解的性能会降低，从而由于稀疏三角求解中行之间的数据依赖性而抑制并行性。因此，GPU 上获得的最佳性能是不完全 LU 分解和 Cholesky 分解，填充为 0，这将作为我们的参考点。

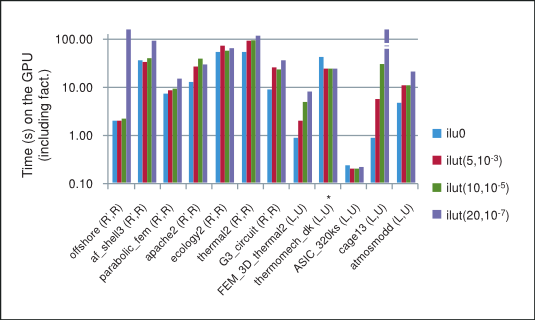
BiCGStab 和 CG 与不完全 LU 分解 Cholesky 预处理的性能

虽然阈值较宽松的不完全分解通常更接近精确分解，因此迭代步数更少，但它们的计算成本也高得多。此外，请注意，即使迭代步数减少，每一步的计算成本也更高。由于这些权衡，迭代方法的总时间（分解时间和迭代求解时间之和）在我们的数值实验中不一定会随着阈值的放宽而减少。

基于 GPU 上使用 csrilu0 预处理器和 CPU 上使用所有四个预处理器的预处理迭代方法所花费的总时间的加速比显示在 图 4 中。请注意，对于我们数值实验中的大多数矩阵，使用 cuSPARSE 和 cuBLAS 库实现的迭代方法确实优于 MKL。

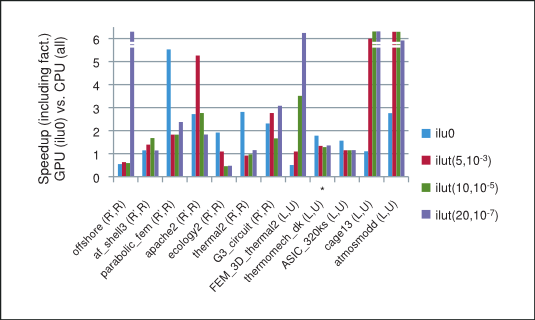
GPU 上预处理 BiCGStab 和 CG（使用 csrilu0）与 CPU 上（使用所有）的速度提升

最后，获得的平均速度提升显示在 图 5 中，其中我们排除了 ilut(10,10^-5) 的 cage13 矩阵的运行，以及 ilut(20,10^-7) 不完全分解的 offshore 和 cage13 矩阵的运行，因为它们的速度提升不成比例。但是，包括这些运行的速度提升显示在同一图中的括号中。因此，我们可以得出结论，不完全 LU 分解和 Cholesky 预处理的 BiCGStab 和 CG 迭代方法在 GPU 上的平均速度提升超过其 CPU 实现的 2 倍。

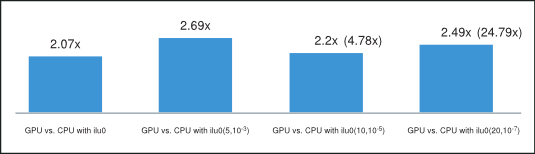
GPU 上 BiCGStab 和 CG（使用 csrilu0）和 CPU 上（使用所有）的平均速度提升

4. 结论

迭代方法的性能在很大程度上取决于手头系数矩阵的稀疏模式。在我们的数值实验中，使用 cuSPARSE 和 cuBLAS 库在 GPU 上实现的不完全 LU 分解和 Cholesky 预处理 BiCGStab 和 CG 迭代方法，其平均速度提升超过 MKL 实现的 2 倍。

稀疏矩阵-向量乘法和三角求解（分为较慢的分析阶段，只需执行一次，以及较快的求解阶段，可以执行多次）是这些迭代方法的基本构建块。事实上，获得的速度提升通常主要受算法求解阶段所花费的时间的影响。

最后，我们指出，使用多右端项将增加可用的并行性，并可能显着提高预处理迭代方法的相对性能。此外，使用 CUDA 并行编程范例开发不完全 LU 分解和 Cholesky 分解可以进一步提高获得的速度提升。

5. 致谢

本白皮书由 Maxim Naumov 为 NVIDIA 公司撰写。

允许出于任何目的复制或影印本作品的全部或部分内容，无需任何费用，但前提是副本上注明本通知以及首页上的完整引文。

6. 参考文献

[1] E. Anderson 和 Y. Saad 并行计算机上求解稀疏三角线性系统, Int. J. High Speed Comput., pp. 73-95, 1989.

[2] R. Barrett, M. Berry, T. F. Chan, J. Demmel, J. Donato, J. Dongarra, V. Eijkhout, R. Pozo, C. Romine, H. van der Vorst, 线性系统求解模板：迭代方法构建块, SIAM, Philadelphia, PA, 1994.

[3] N. Bell 和 M. Garland, 在吞吐量导向处理器上实现稀疏矩阵-向量乘法, Proc. Conf. HPC Networking, Storage and Analysis (SC09), ACM, pp. 1-11, 2009.

[4] A. Greenbaum, 在 NYU Ultracomputer 原型上使用带并行扩展的 Fortran 求解稀疏三角线性系统, Report 99, NYU Ultracomputer Note, New York University, NY, April, 1986.

[5] D. B. Kirk 和 W. W. Hwu, 大规模并行处理器编程：实践方法, Elsevier, 2010.

[6] J. Mayer, 用于求解稀疏三角矩阵线性系统的并行算法, Computing, pp. 291-312 (86), 2009.

[7] R. Mirchandaney, J. H. Saltz 和 D. Baxter, 循环的运行时并行化和调度, IEEE Transactions on Computers, pp. (40), 1991.

[8] M. Naumov, GPU 上预处理迭代方法中稀疏三角线性系统的并行解法, NVIDIA Technical Report, NVR-2011-001, 2011.

[9] J. Nickolls, I. Buck, M. Garland 和 K. Skadron, 使用 CUDA 的可扩展并行编程, Queue, pp. 40-53 (6-2), 2008.

[10] E. Rothberg 和 A. Gupta, 分层内存多处理器上的并行 ICCG - 解决三角求解瓶颈, Parallel Comput., pp. 719-741 (18), 1992.

[11] Y. Saad, 稀疏线性系统的迭代方法, SIAM, Philadelphia, PA, 第 2 版, 2003.

[12] J. H. Saltz, 用于求解多处理器上稀疏三角系统的聚合方法, SIAM J. Sci. Statist. Comput., pp. 123-144 (11), 1990.

[13] J. Sanders 和 E. Kandrot, CUDA by Example：通用 GPU 编程入门, Addison-Wesley, 2010.

[14] M. Wolf, M. Heroux 和 E. Boman, 影响多线程稀疏三角求解性能的因素, 9th Int. Meet. HPC Comput. Sci. (VECPAR), 2010.

[15] S. Williams, L. Oliker, R. Vuduc, J. Shalf, K. Yelick 和 J. Demmel, 新兴多核平台上稀疏矩阵-向量乘法的优化, Parallel Comput., pp. 178-194 (35-3), 2009.

[16] NVIDIA cuSPARSE 和 cuBLAS 库,http://www.nvidia.com/object/cuda_develop.html

[17] Intel Math Kernel Library,http://software.intel.com/en-us/articles/intel-mkl

[18] 佛罗里达大学稀疏矩阵集合, http://www.cise.ufl.edu/research/sparse/matrices/.

7. 通知

7.1. 通知

本文档仅供参考，不得视为对产品的特定功能、条件或质量的保证。NVIDIA Corporation（“NVIDIA”）对本文档中包含的信息的准确性或完整性不作任何明示或暗示的陈述或保证，并且对本文档中包含的任何错误不承担任何责任。NVIDIA 对使用此类信息造成的后果或因使用此类信息而可能导致的侵犯第三方专利或其他权利的行为不承担任何责任。本文档不承诺开发、发布或交付任何材料（如下定义）、代码或功能。

NVIDIA 保留随时对此文档进行更正、修改、增强、改进和任何其他更改的权利，恕不另行通知。

客户在下单前应获取最新的相关信息，并应核实此类信息为最新且完整。

NVIDIA 产品销售受订单确认时提供的 NVIDIA 标准销售条款和条件约束，除非 NVIDIA 和客户的授权代表签署的个别销售协议另有约定（“销售条款”）。NVIDIA 在此明确反对将任何客户通用条款和条件应用于本文件中提及的 NVIDIA 产品的购买。本文件不直接或间接地构成任何合同义务。

NVIDIA 产品并非设计、授权或保证适用于医疗、军事、航空、航天或生命维持设备，也不适用于 NVIDIA 产品的故障或失灵可能合理预期会导致人身伤害、死亡或财产或环境损害的应用。NVIDIA 对在上述设备或应用中包含和/或使用 NVIDIA 产品不承担任何责任，因此，包含和/或使用此类产品由客户自行承担风险。

NVIDIA 不保证或声明基于本文档的产品将适用于任何特定用途。NVIDIA 不一定会对每个产品的所有参数进行测试。客户全权负责评估和确定本文档中包含的任何信息的适用性，确保产品适合并符合客户计划的应用，并为该应用执行必要的测试，以避免应用或产品的缺陷。客户产品设计的缺陷可能会影响 NVIDIA 产品的质量和可靠性，并可能导致超出本文档所包含的附加或不同的条件和/或要求。对于因以下原因引起或可归因于以下原因的任何缺陷、损坏、成本或问题，NVIDIA 不承担任何责任：(i) 以违反本文档的方式使用 NVIDIA 产品，或 (ii) 客户产品设计。

本文件未授予任何 NVIDIA 专利权、版权或其他 NVIDIA 知识产权的明示或暗示许可。NVIDIA 发布的关于第三方产品或服务的信息不构成 NVIDIA 授予的关于使用此类产品或服务的许可，也不构成对其的保证或认可。使用此类信息可能需要获得第三方在其专利或其他知识产权下的许可，或获得 NVIDIA 在其专利或其他知识产权下的许可。

只有在事先获得 NVIDIA 书面批准的情况下，才允许复制本文档中的信息，且复制必须不得更改并完全符合所有适用的出口法律和法规，并附带所有相关的条件、限制和声明。

本文件和所有 NVIDIA 设计规范、参考板、文件、图纸、诊断程序、列表和其他文档（统称为“材料”，单独称为“材料”）均“按原样”提供。NVIDIA 对材料不作任何明示、暗示、法定或其他形式的保证，并明确声明不承担所有关于不侵权、适销性和适用于特定用途的暗示保证。在法律允许的最大范围内，在任何情况下，NVIDIA 均不对因使用本文件而引起的任何损害（包括但不限于任何直接、间接、特殊、附带、惩罚性或后果性损害，无论如何造成，也无论基于何种责任理论）承担责任，即使 NVIDIA 已被告知可能发生此类损害。尽管客户可能因任何原因遭受任何损害，NVIDIA 对本文所述产品的对客户的累计总责任应根据产品的销售条款的规定进行限制。

7.2. OpenCL

OpenCL 是 Apple Inc. 的商标，Khronos Group Inc. 被许可使用。

7.3. 商标

NVIDIA 和 NVIDIA 徽标是 NVIDIA Corporation 在美国和其他国家/地区的商标或注册商标。其他公司和产品名称可能是与其相关的各自公司的商标。