NVIDIA GPU 的浮点数和 IEEE 754 合规性

涵盖与 NVIDIA GPU 相关的最常见问题的白皮书。

许多与浮点精度和合规性相关的问题是 CPU 和 GPU 上常见的困惑来源。 本白皮书的目的是讨论与 NVIDIA GPU 相关的最常见问题，并补充 CUDA C++ 编程指南中的文档。

1. 引言

自从 1985 年广泛采用二进制浮点算术 IEEE 标准（IEEE 754-1985 [1]）以来，几乎所有主流计算系统都已实施该标准，包括 NVIDIA 的 CUDA 架构。 IEEE 754 标准规定了应如何在浮点数中近似算术结果。 在处理不精确的结果时，编程决策会影响精度。 为了在任何特定应用所需的精度下实现最高性能，考虑浮点行为的许多方面非常重要。 在异构计算环境中，在不同类型的硬件上执行操作时，尤其如此。

对于力求实现正确数值算法的 CUDA 程序员来说，了解浮点数的一些复杂性和 NVIDIA 硬件处理浮点数的具体方式显然非常重要。 此外，cuBLAS 和 cuFFT 等库的用户也会发现了解 NVIDIA 如何在底层处理浮点数很有帮助。

我们在 第 2 章 中回顾了浮点数计算的一些基本属性。 我们还讨论了融合乘加运算符，该运算符在 2008 年添加到了 IEEE 754 标准 [2]，并内置于 NVIDIA GPU 的硬件中。 在 第 3 章 中，我们通过计算两个短向量的点积的示例来说明不同实现选择如何影响最终结果的精度。 在 第 4 章 中，我们描述了影响浮点数计算的 NVIDIA 硬件版本和 NVCC 编译器选项。 在 第 5 章 中，我们考虑了 CPU 和 GPU 结果比较的一些问题。 最后，在 第 6 章 中，我们总结了针对处理 GPU 上浮点数相关数值问题的程序员的具体建议。

2. 浮点数

2.1. 格式

浮点数编码和功能在 IEEE 754 标准 [2] 中定义，该标准于 2008 年最后修订。 Goldberg [5] 对浮点数和出现的许多问题进行了很好的介绍。

该标准规定二进制浮点数据应在三个字段上编码：一个符号位字段，后跟指数位，指数位编码按每个格式特定的数值偏差偏移的指数，以及编码有效位数（或小数部分）的位。

为了确保跨平台计算的一致性并交换浮点数据，IEEE 754 定义了基本和交换格式。 32 位和 64 位基本二进制浮点格式对应于 C 数据类型 float 和 double。 它们对应的表示形式具有以下位长度

对于表示有限值的数值数据，符号为负或正，指数字段以 2 为底编码指数，小数部分字段编码有效位数，但不包括最高有效非零位。 例如，值 -192 等于 (-1)¹ x 2⁷ x 1.5，可以表示为具有负号、指数 7 和小数部分 .5。 指数分别偏差 127 和 1023，以允许指数从负数扩展到正数。 因此，指数 7 由位串表示，浮点数为 134，双精度浮点数为 1030。 1. 的整数部分在小数部分中是隐式的。

此外，还保留了表示无穷大和非数字 (NaN) 数据的编码。 IEEE 754 标准 [2] 完整描述了浮点数编码。

鉴于小数部分字段使用有限数量的位，并非所有实数都可以精确表示。 例如，以二进制表示的分数 2/3 的数学值是 0.10101010…，二进制小数点后有无限位。 值 2/3 必须先舍入，才能表示为精度有限的浮点数。 IEEE 754 中规定了舍入规则和舍入模式。 最常用的是舍入到最近或偶数模式（缩写为舍入到最近）。 以这种模式舍入的值 2/3 在二进制中表示为

符号为正，存储的指数值表示指数为 -1。

2.2. 运算和精度

IEEE 754 标准要求支持少量运算。 这些包括算术运算加法、减法、乘法、除法、平方根、融合乘加、余数、转换运算、缩放、符号运算和比较。 对于给定的格式和舍入模式，所有标准实现的这些运算结果都保证相同。

由于浮点数的精度有限，数学算术的规则和属性不直接适用于浮点算术。 例如，下表显示了单精度值 A、B 和 C，以及使用不同结合律计算得出的它们的和的数学精确值。

\(\begin{matrix} A & = & {2^{1} \times 1.00000000000000000000001} \\ B & = & {2^{0} \times 1.00000000000000000000001} \\ C & = & {2^{3} \times 1.00000000000000000000001} \\ {(A + B) + C} & = & {2^{3} \times 1.01100000000000000000001011} \\ {A + (B + C)} & = & {2^{3} \times 1.01100000000000000000001011} \\ \end{matrix}\)

在数学上，(A + B) + C 等于 A + (B + C)。

设 rn(x) 表示 x 上的一个舍入步骤。 根据 IEEE 754，在舍入到最近模式下以单精度浮点算术执行相同的计算，我们得到

\(\begin{matrix} {A + B} & = & {2^{1} \times 1.1000000000000000000000110000...} \\ {\text{rn}(A + B)} & = & {2^{1} \times 1.10000000000000000000010} \\ {B + C} & = & {2^{3} \times 1.0010000000000000000000100100...} \\ {\text{rn}(B + C)} & = & {2^{3} \times 1.00100000000000000000001} \\ {A + B + C} & = & {2^{3} \times 1.0110000000000000000000101100...} \\ {\text{rn}\left( \text{rn}(A + B) + C \right)} & = & {2^{3} \times 1.01100000000000000000010} \\ {\text{rn}\left( A + \text{rn}(B + C) \right)} & = & {2^{3} \times 1.01100000000000000000001} \\ \end{matrix}\)

为了参考，上表也计算了精确的数学结果。 根据 IEEE 754 计算的结果不仅与精确的数学结果不同，而且对应于和 rn(rn(A + B) + C) 和和 rn(A + rn(B + C)) 的结果也彼此不同。 在这种情况下，rn(A + rn(B + C)) 比 rn(rn(A + B) + C) 更接近正确的数学结果。

此示例突出表明，即使所有基本运算都按照 IEEE 754 进行计算，看似相同的计算也可能产生不同的结果。

在这里，运算的执行顺序会影响结果的精度。 结果与主机系统无关。 使用任何微处理器、CPU 或 GPU（支持单精度浮点数）都将获得相同的结果。

2.3. 融合乘加 (FMA)

2008 年，IEEE 754 标准修订为包括融合乘加运算 (FMA)。 FMA 运算计算 \(\text{rn}(X \times Y + Z)\)，仅执行一个舍入步骤。 如果没有 FMA 运算，则必须将结果计算为 \(\text{rn}\left( \text{rn}(X \times Y) + Z \right)\)，执行两个舍入步骤，一个用于乘法，一个用于加法。 由于 FMA 仅使用单个舍入步骤，因此结果计算得更准确。

让我们考虑一个示例，首先使用十进制算术来阐明 FMA 运算的工作原理。 让我们计算 \(x^{2} - 1\)，小数点后精度为四位，或者包括小数点前的首位数字在内的总精度为五位。

对于 \(x = 1.0008\)，正确的数学结果是 \(x^{2} - 1 = 1.60064 \times 10^{- 4}\)。 仅使用小数点后四位的最接近数字是 \(1.6006 \times 10^{- 4}\)。 在这种情况下，\(\text{rn}\left( x^{2} - 1 \right) = 1.6006 \times 10^{- 4}\)，这对应于融合乘加运算 \(\text{rn}\left( x \times x + ( - 1) \right)\)。 另一种方法是分别计算乘法和加法步骤。 对于乘法，\(x^{2} = 1.00160064\)，因此 \(\text{rn}\left( x^{2} \right) = 1.0016\)。 最终结果是 \(\text{rn}\left( \text{rn}\left( x^{2} \right) - 1 \right) = 1.6000 \times 10^{- 4}\)。

分别舍入乘法和加法得到的结果偏差为 0.00064。 相应的 FMA 计算仅偏差 0.00004，其结果最接近正确的数学答案。 结果总结如下

\(\begin{matrix} x & = & 1.0008 & \\ x^{2} & = & 1.00160064 & \\ {x^{2} - 1} & = & {1.60064 \times 10^{- 4}\text{~~}} & \text{真实值} \\ {\text{rn}\left( x^{2} - 1 \right)} & = & {1.6006 \times 10^{- 4}} & \text{融合乘加} \\ {\text{rn}\left( x^{2} \right)} & = & {1.0016 \times 10^{- 4}} & \\ {\text{rn}\left( \text{rn}\left( x^{2} \right) - 1 \right)} & = & {1.6000 \times 10^{- 4}} & \text{乘法，然后加法} \\ \end{matrix}\)

以下是另一个示例，使用二进制单精度值

\(\begin{matrix} A & = & & 2^{0} & {\times 1.00000000000000000000001} \\ B & = & - & 2^{0} & {\times 1.00000000000000000000010} \\ {\text{rn}(A \times A + B)} & = & & 2^{- 46} & {\times 1.00000000000000000000000} \\ {\text{rn}\left( \text{rn}(A \times A) + B \right)} & = & & 0 & \\ \end{matrix}\)

在这种特殊情况下，将 \(\text{rn}\left( \text{rn}(A \times A) + B \right)\) 计算为 IEEE 754 乘法，然后是 IEEE 754 加法，会丢失所有精度位，并且计算结果为 0。 计算 FMA \(\text{rn}(A \times A + B)\) 的替代方法是提供等于数学值的结果。 通常，融合乘加运算比计算一次乘法后跟一次加法产生更准确的结果。 是否选择使用融合运算取决于平台是否提供该运算以及代码的编译方式。

图 1 显示了 CUDA C++ 代码以及与上面示例中的输入 A 和 B 以及运算相对应的输出。 该代码在两个不同的硬件平台上执行：使用 SSE 单精度的 x86 类 CPU 和计算能力为 2.0 的 NVIDIA GPU。 在撰写本文时（2011 年春季），尚无商用 x86 CPU 提供硬件 FMA。 因此，SSE 中单精度计算的结果将为 0。 计算能力为 2.0 的 NVIDIA GPU 提供硬件 FMA，因此默认情况下，执行此代码的结果将更准确。 但是，根据 IEEE 754 标准，这两个结果都是正确的。 代码片段在编译时没有对任何平台使用任何特殊的内在函数或编译器选项。

融合乘加有助于避免在减法抵消期间损失精度。 当符号相反的相似数量级的值相加时，会发生减法抵消。 在这种情况下，许多前导位会被抵消，从而在结果中留下较少的有意义的精度位。 融合乘加在乘法期间计算双倍宽度的积。 因此，即使在加法期间发生减法抵消，积中仍然有足够的有效位来获得精确的结果，而不会损失精度。

3. 点积：精度示例

考虑找到两个短向量 \(\overset{\rightarrow}{a}\) 和 \(\overset{\rightarrow}{b}\) 的点积的问题，这两个向量都包含四个元素。

• \(\overset{\rightharpoonup}{a} = \begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \\ a_{4} \\ \end{bmatrix}\mspace{2mu}\quad\overset{\rightharpoonup}{b} = \begin{bmatrix} b_{1} \\ b_{2} \\ b_{3} \\ b_{4} \\ \end{bmatrix}\quad\overset{\rightharpoonup}{a} \cdot \overset{\rightharpoonup}{b} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3} + a_{4}b_{4}\)

此运算在数学上很容易编写，但其在软件中的实现涉及多个选择。 我们将讨论的所有策略都纯粹使用符合 IEEE 754 的运算。

3.1. 示例算法

我们介绍了三种算法，这些算法在乘法、加法以及可能的融合乘加的组织方式上有所不同。 这些算法在 图 2、图 3 和 图 4 中介绍。 三种算法中的每一种都以图形方式表示。 单个运算显示为圆圈，箭头从自变量指向运算。

计算点积的最简单方法是使用短循环，如 图 2 所示。 乘法和加法是分开进行的。

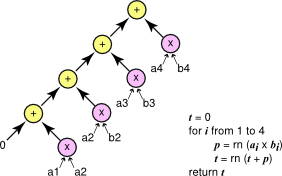
串行方法计算向量点积。

串行方法使用简单的循环以及单独的乘法和加法来计算向量的点积。 最终结果可以表示为 ((((a₁ x b₁) + (a₂ x b₂)) + (a₃ x b₃)) + (a₄ x b₄))。

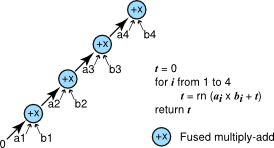
FMA 方法计算向量点积。

FMA 方法使用带有融合乘加的简单循环来计算向量的点积。 最终结果可以表示为 a₄ x b₄ = (a₃ x b₃ + (a₂ x b₂ + (a₁ x b₁ + 0)))。

对算法的简单改进是使用融合乘加在一个步骤中完成乘法和加法，以提高精度。 图 3 显示了此版本。

计算点积的另一种方法是使用分而治之策略，我们首先找到向量的前半部分和后半部分的点积，然后使用加法组合这些结果。 这是一种递归策略； 基本情况是长度为 1 的向量的点积，即单个乘法。 图 4 以图形方式说明了这种方法。 我们将此算法称为并行算法，因为这两个子问题可以并行计算，因为它们没有依赖关系。 但是，该算法不需要并行实现； 它仍然可以使用单个线程实现。

3.2. 比较

所有三种用于计算点积的算法都使用 IEEE 754 算术，并且可以在任何支持 IEEE 标准的系统上实现。 实际上，在多个系统上实现的串行算法将给出完全相同的结果。 FMA 或并行算法的实现也是如此。 但是，通过串行算法的实现计算的结果可能与通过其他两种算法的实现计算的结果不同。

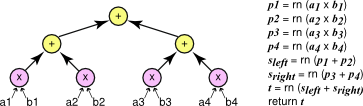
将各个元素乘积归约为最终和的并行方法。

并行方法使用树将各个元素的乘积归约为最终和。 最终结果可以表示为 ((a₁ x b₁) + (a₂ x b₂)) + ((a₃ x b₃) + (a₄ x b₄))。

4. CUDA 和浮点数

NVIDIA 通过每个连续的硬件世代扩展了 GPU 的功能。 当前世代的 NVIDIA 架构，如 Tesla Kxx、GTX 8xx 和 GTX 9xx，支持单精度和双精度，具有 IEEE 754 精度，并且在单精度和双精度中都包含对融合乘加的硬件支持。 在 CUDA 中，GPU 支持的功能编码在计算能力编号中。 运行时库支持函数调用以在运行时确定 GPU 的计算能力； CUDA C++ 编程指南还包括许多不同设备的计算能力表 [7]。

4.1. 计算能力 2.0 及以上

计算能力为 2.0 及以上 的设备支持单精度和双精度 IEEE 754，包括单精度和双精度中的融合乘加。 默认情况下，平方根和除法等运算将产生最接近正确数学结果的浮点值，无论是在单精度还是双精度中。

4.2. 舍入模式

IEEE 754 标准定义了四种舍入模式：舍入到最近、向正无穷舍入、向负无穷舍入和向零舍入。 CUDA 支持所有四种模式。 默认情况下，运算使用舍入到最近。 可以使用下表列出的编译器内在函数来为单个运算选择其他舍入模式。

模式	解释
rn	舍入到最近，平局到偶数
rz	向零舍入
ru	向 \(+ \text{∞}\) 舍入
rd	向 \(- \text{∞}\) 舍入

x + y __fadd_[rn | rz | ru | rd] (x, y)	加法
x * y __fmul_[rn | rz | ru | rd] (x, y)	乘法
fmaf (x, y, z) __fmaf_[rn | rz | ru | rd] (x, y, z)	FMA
1.0f / x __frcp_[rn | rz | ru | rd] (x)	倒数
x / y __fdiv_[rn | rz | ru | rd] (x, y)	除法
sqrtf(x) __fsqrt_[rn | rz | ru | rd] (x)	平方根

x + y __dadd_[rn | rz | ru | rd] (x, y)	加法
x * y __dmul_[rn | rz | ru | rd] (x, y)	乘法
fma (x, y, z) __fma_[rn | rz | ru | rd] (x, y, z)	FMA
1.0 / x __drcp_[rn | rz | ru | rd] (x)	倒数
x / y __ddiv_[rn | rz | ru | rd] (x, y)	除法
sqrtf(x) __dsqrt_[rn | rz | ru | rd] (x)	平方根

4.3. 控制融合乘加

通常，融合乘加运算比执行单独的乘法和加法运算更快、更准确。 但是，有时您可能希望禁用将乘法和加法合并为融合乘加指令。 为了抑制这种优化，可以使用具有显式舍入模式的内在函数来编写乘法和加法，如前面的表格所示。 直接编写为内在函数的运算保证保持独立，并且不会合并到融合乘加指令中。 也可以通过编译器标志禁用 FMA 合并。

4.4. 编译器标志

与 IEEE 754 运算相关的编译器标志为 -ftz={true|false}、-prec-div={true|false} 和 -prec-sqrt={true|false}。 这些标志控制计算能力为 2.0 或更高版本的设备上的单精度运算。

模式	标志
IEEE 754 模式（默认）	-ftz=false -prec-div=true -prec-sqrt=true
快速模式	-ftz=true -prec-div=false -prec-sqrt=false

默认的 IEEE 754 模式 意味着单精度运算已正确舍入并支持非规格化数，如 IEEE 754 标准中所述。 在快速模式下，非规格化数将刷新为零，并且除法和平方根运算不会计算到最接近的浮点值。 这些标志对双精度或计算能力低于 2.0 的设备没有影响。

4.5. 与 x86 的差异

NVIDIA GPU 与 x86 架构的不同之处在于，舍入模式编码在每个浮点指令中，而不是动态使用浮点控制字。 不支持浮点异常的陷阱处理程序。 在 GPU 上，没有状态标志指示计算何时溢出、下溢或涉及不精确的算术。 与 SSE 一样，每个 GPU 运算的精度都编码在指令中（对于 x87，精度由浮点控制字动态控制）。

5. 异构环境的考量

5.1. 数学函数精度

到目前为止，我们只考虑了简单的数学运算，如加法、乘法、除法和平方根。 这些运算足够简单，以至于计算最佳浮点结果（例如，舍入到最近的最接近结果）是合理的。 对于其他数学运算，计算最佳浮点结果更困难。

这个问题称为制表者的困境。 为了保证正确舍入的结果，通常仅将函数计算到固定的高精度是不够的。 在精度较低的舍入步骤中，高精度结果中的误差仍然可能影响舍入步骤。

可以通过进行数学分析和形式证明 [4] 来解决特定函数的困境，但大多数数学库选择放弃保证正确舍入。 相反，它们提供了数学函数的实现，并记录了函数在输入范围内的相对误差界限。 例如，CUDA 中的双精度 sin 函数保证在正确舍入结果的最后一位 (ulp) 的 2 个单位内是准确的。 换句话说，计算结果与数学结果之间的差异最多为 ±2，相对于浮点结果的小数部分的最低有效位位置而言。

对于大多数输入，sin 函数会产生正确舍入的结果。 以 图 6 中所示的 C 代码序列为例。 我们在 64 位 x86 平台上使用 gcc 版本 4.4.3 (Ubuntu 4.3.3-4ubuntu5) 编译了代码序列。

这表明，使用通用库计算 cos(5992555.0) 的结果会因代码是以 32 位模式还是 64 位模式编译而异。

结果是，不能期望不同的数学库为给定的输入计算出完全相同的结果。 这也适用于 GPU 编程。 为 GPU 编译的函数将使用 NVIDIA CUDA 数学库实现，而为 CPU 编译的函数将使用主机编译器数学库实现（例如，Linux 上的 glibc）。 因为这些实现是独立的，并且都不能保证正确舍入，所以结果通常会略有不同。

5.2. x87 和 SSE

C 编译器的一个不幸现实是，它们通常不擅长保留浮点运算的 IEEE 754 语义 [6]。 这在支持 x87 和 SSE 运算的平台上尤其令人困惑。 就像 CUDA 运算一样，SSE 运算对单精度或双精度值执行，而 x87 运算通常使用额外的内部 80 位精度格式。 有时，使用 x87 进行计算的结果可能取决于中间结果是分配给寄存器还是存储到内存。 存储到内存的值将舍入到声明的精度（例如，float 为单精度，double 为双精度）。 保存在寄存器中的值可以保持扩展精度。 此外，x87 指令通常默认用于 32 位编译，但 SSE 指令通常默认用于 64 位编译。

由于这些问题，有时很难保证 CPU 上的特定精度级别。 在将 CPU 结果与 GPU 上计算的结果进行比较时，通常最好使用 SSE 指令进行比较。 SSE 指令遵循单精度和双精度的 IEEE 754。

在没有 SSE 的 32 位 x86 目标上，使用 volatile 声明变量并强制将浮点值存储到内存（Visual Studio 中的 /Op 和 gcc 中的 -ffloat-store）可能会有所帮助。 这会将结果从扩展精度寄存器移动到内存，在内存中，精度恰好是单精度或双精度。 或者，可以使用汇编指令 fldcw 或编译器选项（如 gcc 中的 -mpc32 或 -mpc64）更新 x87 控制字，以将精度设置为 24 或 53 位。

5.3. 核心数量

正如我们在 第 3 节 中所示，使用 IEEE 754 算术计算的最终值可能取决于实现选择，例如是否使用融合乘加或者加法是以串行还是并行方式组织。 这些差异会影响 CPU 和 GPU 上的计算。

造成这些差异的一种方式是由于计算中涉及的并发线程数量不同。在 GPU 上，一种常见的设计模式是让一个区块中的所有线程协同工作，对区块内的数据进行并行归约，然后对来自每个区块的结果进行串行归约。更改每个区块的线程数会重新组织归约；如果归约是加法，那么更改会重新排列长串加法运算中的括号。

即使 CPU 和 GPU 上使用了相同的通用策略（例如并行归约），GPU 上的线程数与 CPU 上的线程数也常常大相径庭。例如，GPU 实现可能会启动每个区块 128 个线程的区块，而 CPU 实现可能总共使用 4 个线程。

5.4. 验证 GPU 结果

对于给定的精度，相同的输入在 CPU 和 GPU 上对于单个 IEEE 754 操作会给出相同的结果。正如我们已经解释过的，有很多原因导致在 CPU 和 GPU 上可能不会执行相同的操作序列。GPU 具有融合乘加运算，而 CPU 没有。并行化算法可能会重新排列操作，从而产生不同的数值结果。CPU 可能会以高于预期的精度计算结果。最后，许多常见的数学函数不要求 IEEE 754 标准进行正确舍入，因此不应期望在不同实现之间产生相同的结果。

当将数值代码从 CPU 移植到 GPU 时，当然有理由使用 x86 CPU 结果作为参考。但是，必须仔细解释 CPU 结果和 GPU 结果之间的差异。差异并不自动证明 GPU 计算的结果是错误的，或者 GPU 存在问题。

以高精度计算结果，然后与以较低精度计算的结果进行比较，有助于查看较低精度是否适用于特定应用。但是，将高精度结果舍入为较低精度并不等同于以较低精度执行整个计算。当使用 x87 并将结果与 GPU 进行比较时，这有时会成为一个问题。对于某些或所有操作，CPU 的结果可能会以出乎意料的高扩展精度计算。GPU 结果将仅使用单精度或双精度计算。

6. 具体建议

我们已经涵盖的关键点如下：

使用融合乘加运算符。

GPU 上的融合乘加运算符具有高性能，并提高了计算的精度。在 CUDA 程序中，无需特殊的标志或函数调用即可获得此好处。请理解，硬件融合乘加运算在 CPU 上尚不可用，这可能会导致数值结果的差异。

仔细比较结果。

即使在严格的 IEEE 754 运算世界中，诸如括号的组织或线程计数等微小细节也可能会影响最终结果。在进行不同实现之间的比较时，请考虑这一点。

了解您的 GPU 的功能。

数值功能编码在您的 GPU 的计算能力编号中。计算能力为 2.0 及更高版本的设备能够进行符合 IEEE 754 标准的单精度和双精度算术运算，并且具有用于执行单精度和双精度融合乘加运算的硬件单元。

充分利用 CUDA 数学库函数。

这些函数在 CUDA C++ 编程指南 [7] 中有文档记录。数学库包括 C99 标准 [3] 中列出的所有数学函数以及一些其他有用的函数。这些函数经过调整，在性能和精度之间取得了合理的折衷。我们不断努力提高数学库功能的质量。如果您需要我们未提供的任何函数，或者我们的任何函数的精度或性能不能满足您的需求，请告知我们。请在 NVIDIA CUDA 论坛 1 中留言，或加入注册开发者计划 2 并提交包含您反馈的错误报告。

7. 致谢

本文由 Nathan Whitehead 和 Alex Fit-Florea 为 NVIDIA 公司撰写。

感谢 Ujval Kapasi、Kurt Wall、Paul Sidenblad、Massimiliano Fatica、Everett Phillips、Norbert Juffa 和 Will Ramey 提供的有益评论和建议。

允许在任何用途下复制本文档的全部或部分数字或纸质副本，无需费用，前提是副本带有此声明以及首页上的完整引文。

8. 参考文献

[1] ANSI/IEEE 754-1985. American National Standard - IEEE Standard for Binary Floating-Point Arithmetic. American National Standards Institute, Inc., New York, 1985.

[2] IEEE 754-2008. IEEE 754–2008 Standard for Floating-Point Arithmetic. August 2008.

[3] ISO/IEC 9899:1999(E). Programming languages - C. American National Standards Institute, Inc., New York, 1999.

[4] Catherine Daramy-Loirat, David Defour, Florent de Dinechin, Matthieu Gallet, Nicolas Gast, and Jean-Michel Muller. CR-LIBM: A library of correctly rounded elementary functions in double-precision, February 2005.

[5] David Goldberg. What every computer scientist should know about floating-point arithmetic. ACM Computing Surveys, March 1991. Edited reprint available at: http://download.oracle.com/docs/cd/E19957-01/806-3568/ncg_goldberg.html.

[6] David Monniaux. The pitfalls of verifying floating-point computations. ACM Transactions on Programming Languages and Systems, May 2008.

[7] NVIDIA. CUDA C++ Programming Guide Version 10.2, 2019.

9. 声明

9.1. 声明

本文档仅供参考，不应被视为对产品的特定功能、条件或质量的保证。NVIDIA 公司（“NVIDIA”）对本文档中包含信息的准确性或完整性不做任何明示或暗示的陈述或保证，并且对本文档中包含的任何错误不承担任何责任。NVIDIA 对因使用此类信息而造成的后果或使用，或因使用此类信息而可能导致的侵犯专利或第三方的其他权利不承担任何责任。本文档不构成对开发、发布或交付任何材料（如下定义）、代码或功能的承诺。

NVIDIA 保留随时对本文档进行更正、修改、增强、改进和任何其他更改的权利，恕不另行通知。

客户在下订单前应获取最新的相关信息，并应验证此类信息是最新且完整的。

NVIDIA 产品的销售受 NVIDIA 在订单确认时提供的标准销售条款和条件的约束，除非 NVIDIA 和客户的授权代表签署的单独销售协议（“销售条款”）另有约定。NVIDIA 在此明确反对将任何客户通用条款和条件应用于购买本文档中引用的 NVIDIA 产品。本文档不直接或间接地形成任何合同义务。

NVIDIA 产品并非设计、授权或保证适用于医疗、军事、航空、航天或生命支持设备，也不适用于 NVIDIA 产品的故障或失灵可能合理预期会导致人身伤害、死亡或财产或环境损害的应用。对于在上述设备或应用中包含和/或使用 NVIDIA 产品，NVIDIA 不承担任何责任，因此，包含和/或使用此类产品由客户自行承担风险。

NVIDIA 不表示或保证基于本文档的产品将适用于任何特定用途。NVIDIA 不一定对每个产品的所有参数进行测试。客户全权负责评估和确定本文档中包含的任何信息的适用性，确保产品适合并满足客户计划的应用，并为该应用执行必要的测试，以避免应用或产品的缺陷。客户产品设计的缺陷可能会影响 NVIDIA 产品的质量和可靠性，并可能导致超出本文档中包含的附加或不同的条件和/或要求。NVIDIA 对任何可能基于或归因于以下原因的缺陷、损坏、成本或问题不承担任何责任：(i) 以违反本文档的任何方式使用 NVIDIA 产品或 (ii) 客户产品设计。

本文档未授予任何 NVIDIA 专利权、版权或其他 NVIDIA 知识产权下的任何明示或暗示的许可。NVIDIA 发布的有关第三方产品或服务的信息不构成 NVIDIA 授予的使用此类产品或服务的许可，也不构成 NVIDIA 对其的保证或认可。使用此类信息可能需要从第三方获得第三方专利或其他知识产权下的许可，或从 NVIDIA 获得 NVIDIA 专利或其他知识产权下的许可。

仅当事先获得 NVIDIA 书面批准，并在未经修改且完全遵守所有适用的出口法律和法规，并附带所有相关的条件、限制和声明的情况下，才允许复制本文档中的信息。

本文档以及所有 NVIDIA 设计规范、参考板、文件、图纸、诊断程序、列表和其他文档（统称为“材料”，单独及合称）均“按原样”提供。NVIDIA 对这些材料不做任何明示、暗示、法定或其他方面的保证，并明确声明不承担任何关于不侵权、适销性和适用于特定用途的默示保证。在法律未禁止的范围内，在任何情况下，NVIDIA 均不对因使用本文档而引起的任何损害（包括但不限于任何直接、间接、特殊、附带、惩罚性或后果性损害，无论因何种原因造成，也无论基于何种责任理论）承担责任，即使 NVIDIA 已被告知可能发生此类损害。尽管客户可能因任何原因遭受任何损害，NVIDIA 对客户就本文所述产品承担的总体和累积责任应根据产品的销售条款进行限制。

9.2. OpenCL

OpenCL 是 Apple Inc. 的商标，已授权 Khronos Group Inc. 使用。

9.3. 商标

NVIDIA 和 NVIDIA 徽标是 NVIDIA 公司在美国和其他国家/地区的商标或注册商标。其他公司和产品名称可能是与其相关的各自公司的商标。

1

https://forums.nvidia.com/index.php?showforum=62

2

https://developer.nvidia.com/join-nvidia-registered-developer-program